题目内容
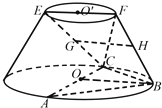
【题目】如图,在圆锥PO中,已知![]() ,圆O的直径
,圆O的直径![]() ,C是弧AB的中点,D为AC的中点.
,C是弧AB的中点,D为AC的中点.

(1)求异面直线PD和BC所成的角的正切值;
(2)求直线OC和平面PAC所成角的正弦值.
【答案】(1)2;(2)![]()
【解析】
试题(1)异面直线所成的角,往往通过平移转化到一个三角形内求解.本题转化到直角三角形PDO中求解.(2)直线与平面所成的角,应先作出直线在平面内的射影,则斜线与射影所成的角即为所求.本题过点O向平面PAC作垂线,则![]() 即为直线与平面所成的角,进而求出其正弦值.
即为直线与平面所成的角,进而求出其正弦值.
试题解析:(1)![]() O,D分别是AB和AC的中点
O,D分别是AB和AC的中点
![]() OD//BC
OD//BC
![]() 异面直线PD和BC所成的角为∠PDO
异面直线PD和BC所成的角为∠PDO
在△ABC中,![]() 的中点
的中点
![]() 又
又![]()
![]()
![]()
(2)因为![]()
又![]() 所以
所以![]()
又![]() 所以平面
所以平面![]() 在平面
在平面![]() 中,过
中,过![]() 作
作![]()
则![]() 连结
连结![]() ,则
,则![]() 是
是![]() 上的射影,
上的射影,
所以![]() 是直线
是直线![]() 和平面
和平面![]() 所成的角.
所成的角.
在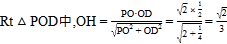
在![]()

练习册系列答案
相关题目