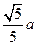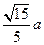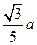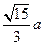题目内容
二面角α—a—β是120°的二面角,P是该角内的一点.P到α、β的距离分别为a,b.求:P到棱a的距离.
设PA⊥α于A,PB⊥β于B.过PA与PB作平面r与α交于AO,与β交于OB,
∵PA⊥α,PB⊥β,∴a⊥PA,且a⊥PB
∴a⊥面r,∴a⊥PO,PO的长为P到棱a的距离.
且∠AOB是二面角之平面角,∠AOB =120°
∴∠APB = 60°,PA = a,PB = b.
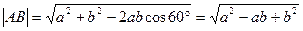
∵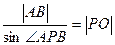 ,
,
∴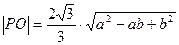 .
.
∵PA⊥α,PB⊥β,∴a⊥PA,且a⊥PB
∴a⊥面r,∴a⊥PO,PO的长为P到棱a的距离.
且∠AOB是二面角之平面角,∠AOB =120°
∴∠APB = 60°,PA = a,PB = b.
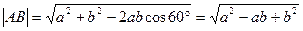
∵
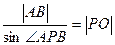 ,
,∴
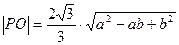 .
.
练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 的直线的方程.
的直线的方程. 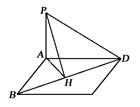
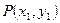 、
、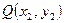 之间的“直角距离”为
之间的“直角距离”为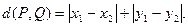 若
若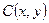 到点
到点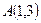 、
、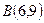 的“直角距离”相等,其中实
的“直角距离”相等,其中实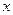 、
、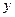 满足
满足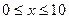 、
、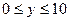 ,则所有满足条件的点
,则所有满足条件的点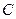 的轨迹的长度之和为 .
的轨迹的长度之和为 .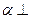 平面
平面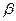 ,
,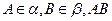 与两平面
与两平面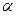 、
、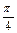 和
和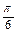 。过A、B分别作两平面交线的垂线,垂足为
。过A、B分别作两平面交线的垂线,垂足为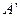 、
、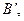 若AB=12,则
若AB=12,则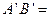
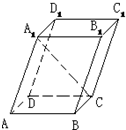
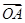 、
、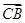 夹角θ的余弦值为( )
夹角θ的余弦值为( )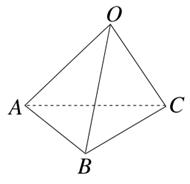
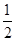
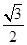
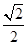
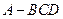 中,
中,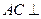 底面
底面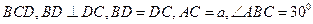 ,
,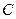 到平面
到平面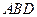 的距离是( )
的距离是( )