题目内容
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 ,其中
,其中![]() 为参数,在以坐标原点
为参数,在以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() , 直线
, 直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点, ![]() 为线段
为线段![]() 的中点.求点
的中点.求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
【答案】(1) 曲线![]() 的普通方程为
的普通方程为![]() 直线
直线![]() 的直角坐标方程为
的直角坐标方程为![]() ;(2) 最大值为
;(2) 最大值为![]() .
.
【解析】试题分析:(1)首先利用关系式把极坐标转化成直角坐标,进一步把极坐标方程转化成直角坐标方程.
(2)先把直角坐标方程转化成参数方程,进一步利用点到直线的距离公式,再利用三角函数的最值求出结果.
试题解析:
(1)∵直线![]() 的极坐标方程为
的极坐标方程为![]() ,即
,即![]() .
.
由![]() ,
, ![]() ,可得直线
,可得直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
将曲线![]() 的参数方程
的参数方程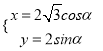 消去参数
消去参数![]() ,得曲线
,得曲线![]() 的普通方程为
的普通方程为![]() .
.
(2)设![]()
![]() .
.
点![]() 的极坐标
的极坐标![]() 化为直角坐标为
化为直角坐标为![]() .
.
则![]() .
.
∴点![]() 到直线
到直线![]() 的距离
的距离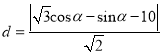
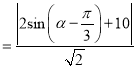
![]() .
.
当![]() ,即
,即![]() 时,等号成立.
时,等号成立.
∴点![]() 到直线
到直线![]() 的距离的最大值为
的距离的最大值为![]() .
.

练习册系列答案
相关题目
【题目】柴静《穹顶之下》的播出,让大家对雾霾天气的危害有了更进一步的认识,对于雾霾天气的研究也渐渐活跃起来,某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据:
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测燃放烟花爆竹的天数为![]() 的雾霾天数.
的雾霾天数.