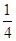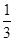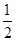题目内容
(2013•浙江)设a,b∈R,若x≥0时恒有0≤x4﹣x3+ax+b≤(x2﹣1)2,则ab等于 _________ .
﹣1
验证发现,
当x=1时,将1代入不等式有0≤a+b≤0,所以a+b=0,
当x=0时,可得0≤b≤1,结合a+b=0可得﹣1≤a≤0
令f(x)=x4﹣x3+ax+b,即f(1)=a+b=0
又f′(x)=4x3﹣3x2+a,f′′(x)=12x2﹣6x,
令f′′(x)>0,可得x> ,则f′(x)=4x3﹣3x2+a在[0,
,则f′(x)=4x3﹣3x2+a在[0, ]上减,在[
]上减,在[ ,+∞)上增
,+∞)上增
又﹣1≤a≤0,所以f′(0)=a<0,f′(1)=1+a≥0
又x≥0时恒有0≤x4﹣x3+ax+b,结合f(1)=a+b=0知,1必为函数f(x)=x4﹣x3+ax+b的极小值点,也是最小值点
故有f′(1)=1+a=0,由此得a=﹣1,b=1
故ab=﹣1
故答案为﹣1
当x=1时,将1代入不等式有0≤a+b≤0,所以a+b=0,
当x=0时,可得0≤b≤1,结合a+b=0可得﹣1≤a≤0
令f(x)=x4﹣x3+ax+b,即f(1)=a+b=0
又f′(x)=4x3﹣3x2+a,f′′(x)=12x2﹣6x,
令f′′(x)>0,可得x>
 ,则f′(x)=4x3﹣3x2+a在[0,
,则f′(x)=4x3﹣3x2+a在[0, ]上减,在[
]上减,在[ ,+∞)上增
,+∞)上增又﹣1≤a≤0,所以f′(0)=a<0,f′(1)=1+a≥0
又x≥0时恒有0≤x4﹣x3+ax+b,结合f(1)=a+b=0知,1必为函数f(x)=x4﹣x3+ax+b的极小值点,也是最小值点
故有f′(1)=1+a=0,由此得a=﹣1,b=1
故ab=﹣1
故答案为﹣1

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
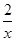 +ln x,则( )
+ln x,则( ) 为f(x)的极大值点
为f(x)的极大值点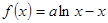 .
.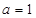 时,求
时,求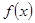 的极值;
的极值;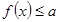 对
对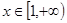 恒成立,求实数
恒成立,求实数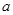 的取值范围.
的取值范围.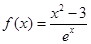 的图象是( )
的图象是( )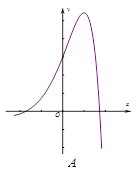
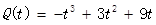 ,则这个工人从8:00到12:00何时的工作效率最高?
,则这个工人从8:00到12:00何时的工作效率最高?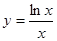 的最大值为( )
的最大值为( )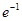
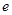
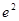
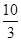
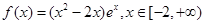 ,
,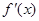 是函数
是函数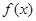 的导函数,且
的导函数,且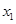 和
和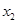 (
(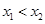 ),则
),则


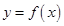 是奇函数,当
是奇函数,当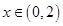 时,
时,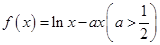 ,当
,当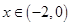 时,
时,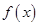 的最小值为1,则
的最小值为1,则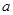 的值等于( )
的值等于( )