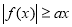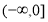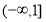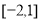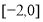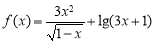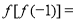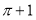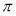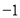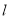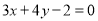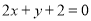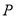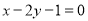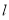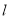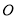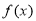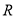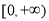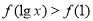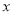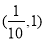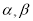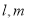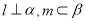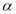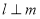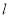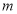题目内容
定义:对于函数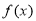 ,若在定义域内存在实数
,若在定义域内存在实数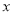 ,满足
,满足 ,则称
,则称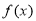 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数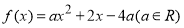 ,试判断
,试判断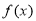 是否为定义域
是否为定义域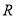 上的“局部奇函数”?若是,求出满足
上的“局部奇函数”?若是,求出满足 的
的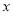 的值;若不是,请说明理由;
的值;若不是,请说明理由;
(2)若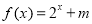 是定义在区间
是定义在区间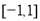 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数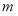 的取值范围;
的取值范围;
(3)若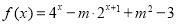 为定义域
为定义域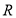 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数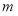 的取值范围.
的取值范围.
(1)是“局部奇函数”;(2) ;(3)
;(3) .
.
【解析】
试题分析:(1)利用局部奇函数的定义,建立方程关系,然后判断方程是否有解,有解则是“局部奇函数”,若无解,则不是;(2)(3)都是利用“局部奇函数的定义”,建立方程关系,并将方程有解的问题转化成二次方程根的分布问题,从而求出各小问参数的取值范围.
试题解析:(1)当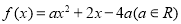 ,方程
,方程 即
即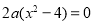 ,有解
,有解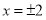
所以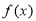 为“局部奇函数”
为“局部奇函数”
(2)法一:当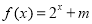 时,
时, 可化为
可化为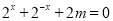
因为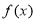 的定义域为
的定义域为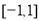 ,所以方程
,所以方程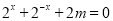 在
在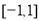 上有解
上有解
令 ,则
,则 ,设
,设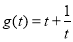 ,则
,则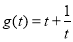 在
在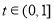 上为减函数,在
上为减函数,在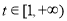 上为增函数,所以当
上为增函数,所以当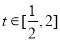 时,
时,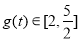 ,所以
,所以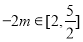 ,即
,即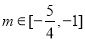 ;
;
法二:当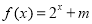 时,
时, 可化为
可化为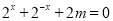
因为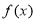 的定义域为
的定义域为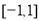 ,所以方程
,所以方程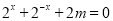 即
即 在
在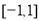 上有解
上有解
令 ,则关于
,则关于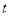 的二次方程
的二次方程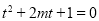 在
在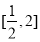 上有解即可保证
上有解即可保证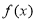 为“局部奇函数”
为“局部奇函数”
设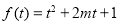 ,当方程
,当方程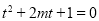 在
在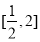 上只有一解时,须满足
上只有一解时,须满足 或
或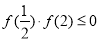 ,解之得
,解之得 (舍去,因为此时方程在区间
(舍去,因为此时方程在区间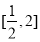 有两解,不符合这种情况)或
有两解,不符合这种情况)或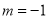 ;
;
当方程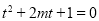 在
在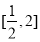 上两个不等的实根时,须满足
上两个不等的实根时,须满足
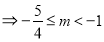 ,综上可知
,综上可知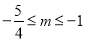 ;
;
(3)当 为定义域
为定义域 上的“局部奇函数”时
上的“局部奇函数”时
 ,可化为
,可化为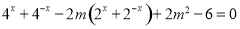 ,
,
令 则
则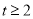 ,
,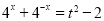
从而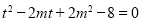 在
在 有解,即可保证
有解,即可保证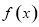 为“局部奇函数”
为“局部奇函数”
令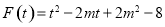 ,则
,则
①当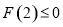 时,
时,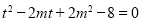 在
在 有解,即
有解,即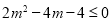 ,解得
,解得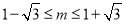
②当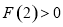 时,
时,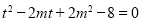 在
在 有解等价于
有解等价于
解得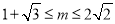 ;综上可知
;综上可知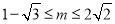 .
.
考点:1.新定义;2.函数与方程;3.一元二次方程根的分布问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目