题目内容
过点（1，2）且与直线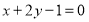
平行的直线方程是 .
【解析】
试题分析：与直线
平行的直线方程可设为
，把点（1，2）代入，求得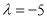
，所以直线方程为.
考点：直线方程、两直线的位置关系.
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
过点（1，2）且与直线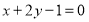平行的直线方程是 .
【解析】
试题分析：与直线平行的直线方程可设为，把点（1，2）代入，求得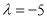，所以直线方程为.
考点：直线方程、两直线的位置关系.
阅读快车系列答案
