题目内容
9.若函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=$\left\{\begin{array}{l}{lo{g}_{2}(x+1),x∈[0,1)}\\{|x-3|-1,x∈[1,+∞)}\end{array}\right.$,则函数g(x)=f(x)-$\frac{1}{3}$的所有零点之和为$\root{3}{2}$-1.分析 根据分段函数的表达式结合函数奇偶性的性质求出函数的解析式,作出函数f(x)的图象,解方程即可.
解答 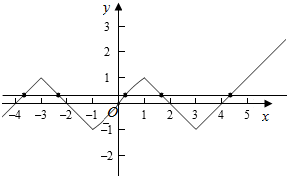 解:∵函数f(x)是定义在R上的奇函数,
解:∵函数f(x)是定义在R上的奇函数,
∴若x∈(-1,0],则-x∈[0,1),
则f(-x)=log2(-x+1)=-f(x),
即f(x)=-log2(-x+1),x∈(-1,0],
若x∈(-∞,-1],则-x∈[1,+∞),
则f(-x)=|-x-3|-1=|x+3|-1=-f(x),
即f(x)=1-|x+3|,x∈(-∞,-1],
作出f(x)的图象如图:
由g(x)=f(x)-$\frac{1}{3}$=0得f(x)=$\frac{1}{3}$,
由图象知,当x∈[0,1)时,由log2(x+1)=$\frac{1}{3}$得x+1=${2}^{\frac{1}{3}}=\root{3}{2}$,即x=$\root{3}{2}$-1,
当x∈[1,+∞)时,由|x-3|-1=$\frac{1}{3}$得|x-3|=$\frac{4}{3}$,即x=$\frac{13}{3}$或$\frac{5}{3}$,
当x∈(-∞,-1]时,由1-|x+3|=$\frac{1}{3}$得|x+3|=$\frac{2}{3}$,即x=-$\frac{11}{3}$或-$\frac{7}{3}$,
故所有的零点之和为$\frac{13}{3}$+$\frac{5}{3}$-$\frac{11}{3}$-$\frac{7}{3}$+$\root{3}{2}$-1=$\root{3}{2}$-1,
故答案为:$\root{3}{2}$-1
点评 本题主要考查函数零点和方程之间的关系,根据函数奇偶性的性质求出函数的解析式是解决本题的关键.注意利用数形结合.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
4.1.2log6$\sqrt{2}$+3log6$\root{3}{3}$=( )
| A. | 0 | B. | 1 | C. | 6 | D. | log6$\frac{2}{3}$ |
11.若一位学生把英语单词“error”中字母的拼写错了,则可能出现错误的种数是( )
| A. | 9 | B. | 10 | C. | 19 | D. | 20 |
9.阅读程序框图,如果输出i=5,那么在空白矩形框中填入的语句为( )
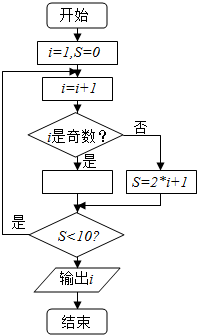

| A. | S=2*i+4 | B. | S=2*i-1 | C. | S=2*i-2 | D. | S=2*i |