题目内容
已知 为奇函数
为奇函数 的极大值点,
的极大值点,
(1)求 的解析式;
的解析式;
(2)若 在曲线
在曲线 上,过点
上,过点 作该曲线的切线,求切线方程.
作该曲线的切线,求切线方程.
 为奇函数
为奇函数 的极大值点,
的极大值点,(1)求
 的解析式;
的解析式;(2)若
 在曲线
在曲线 上,过点
上,过点 作该曲线的切线,求切线方程.
作该曲线的切线,求切线方程.(1) 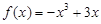 ;
;
(2) 切线方程为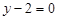 或
或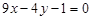
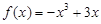 ;
;(2) 切线方程为
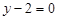 或
或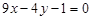
本试题主要是考查而来导数在研究函数中的运用,导数的几何意义的运用,导数的极值的运用。
(1)因为 为奇函数
为奇函数 的极大值点,可知参数a,b的值,得到解析式。
的极大值点,可知参数a,b的值,得到解析式。
(2)由(1)知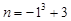 ,设切点为
,设切点为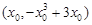 ,则切线方程为
,则切线方程为
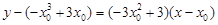 .
.
 点在切线上,有
点在切线上,有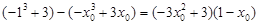 解方程得到切线的坐标,进而得到方程。
解方程得到切线的坐标,进而得到方程。
解:(1) 为奇函数,故
为奇函数,故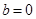 .
.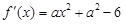 .
.  分
分
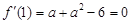 ,得
,得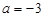 或
或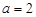 .
.  分
分
当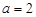 时,
时, 为
为 的极小值点,与已知矛盾,舍去.
的极小值点,与已知矛盾,舍去.
故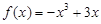 .
.  分
分
(2)由(1)知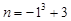 ,设切点为
,设切点为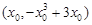 ,则切线方程为
,则切线方程为
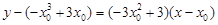 .
.
 点在切线上,有
点在切线上,有
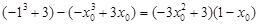 ,
,
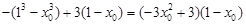 ,
,
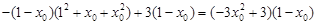 ,
,
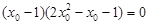 ,
,
即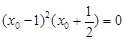 .
.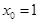 或
或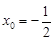 ,此时原曲线有两条切线.
,此时原曲线有两条切线.  分
分
切线方程为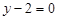 或
或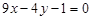 .
. 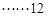 分
分
(1)因为
 为奇函数
为奇函数 的极大值点,可知参数a,b的值,得到解析式。
的极大值点,可知参数a,b的值,得到解析式。(2)由(1)知
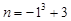 ,设切点为
,设切点为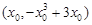 ,则切线方程为
,则切线方程为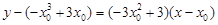 .
. 点在切线上,有
点在切线上,有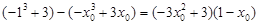 解方程得到切线的坐标,进而得到方程。
解方程得到切线的坐标,进而得到方程。解:(1)
 为奇函数,故
为奇函数,故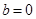 .
.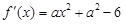 .
. 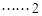 分
分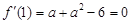 ,得
,得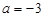 或
或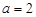 .
.  分
分当
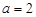 时,
时, 为
为 的极小值点,与已知矛盾,舍去.
的极小值点,与已知矛盾,舍去.故
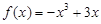 .
.  分
分(2)由(1)知
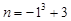 ,设切点为
,设切点为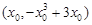 ,则切线方程为
,则切线方程为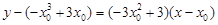 .
. 点在切线上,有
点在切线上,有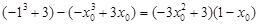 ,
,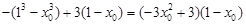 ,
,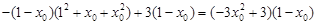 ,
,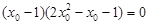 ,
,即
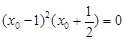 .
.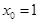 或
或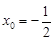 ,此时原曲线有两条切线.
,此时原曲线有两条切线.  分
分切线方程为
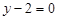 或
或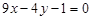 .
. 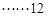 分
分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
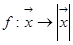 下,2的一个原像可以是( )
下,2的一个原像可以是( ) 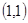
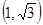

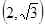
 ,②
,② ,③
,③
 ,④
,④ ,其中是同一函数的是______________(写出所有符合要求的函数序号)
,其中是同一函数的是______________(写出所有符合要求的函数序号)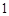 ,高为
,高为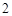 和
和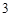 的两矩形所构
的两矩形所构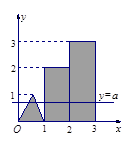
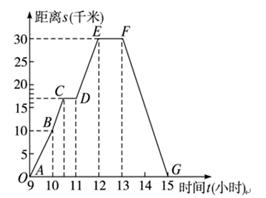
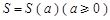 是图中阴影部分介于平行线
是图中阴影部分介于平行线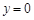 及
及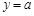 之间的那一部分的面积,则函数
之间的那一部分的面积,则函数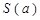 的图象大致为
的图象大致为 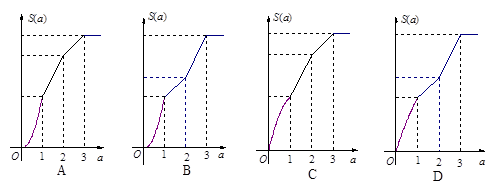
 与
与
 分别相交于点
分别相交于点 ,且曲线
,且曲线 和
和 在点
在点 的值;
的值; 为
为 的导函数,若对于任意的
的导函数,若对于任意的 ,
, 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 倍时,当
倍时,当 时,若函数
时,若函数 的最小值恰为
的最小值恰为 的最小值,求实数
的最小值,求实数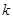 的值
的值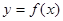 是奇函数,当
是奇函数,当 时,
时, ,则
,则
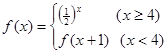 ,则
,则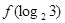 等于( )
等于( )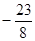
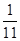
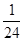
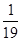
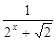 ,利用课本中推导等差数列前n项和的公式的方法,
,利用课本中推导等差数列前n项和的公式的方法,