题目内容
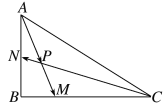
【题目】△ABC的三个内角A、B、C的对边分别是a、b、c,其面积S=a2﹣(b﹣c)2 . 若a=2,则BC边上的中线长的取值范围是 .
【答案】(1,4]
【解析】解:∵S=a2﹣(b﹣c)2=a2﹣b2﹣c2+2bc,
b2+c2﹣a2=2bccosA,
S= ![]() ,
,
∴2bc(1﹣cosA)= ![]() bcsinA,
bcsinA,
∴sinA=4﹣4cosA,
又∵sin2A+cos2A=1,
∴cosA= ![]() ,sinA=
,sinA= ![]() .
.
由正弦定理得 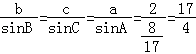 ,
,
∴b= ![]() ,c=
,c= ![]() .
.
设BC的中点为D,则CD= ![]() .
.
在△ACD中,由余弦定理得AD2=CD2+AC2﹣2ACCDcosC=1+ ![]() sin2B﹣
sin2B﹣ ![]() cosC.
cosC.
∵cosC=﹣cos(A+B)=sinAsinB﹣cosAcosB= ![]() ,
,
∴AD2=1+ ![]() sin2B﹣
sin2B﹣ ![]() (
( ![]() )=
)= ![]() sin2B+
sin2B+ ![]() sinBcosB+1=
sinBcosB+1= ![]() ×
× ![]() +
+ ![]() sin2B+1=
sin2B+1= ![]() sin2B﹣
sin2B﹣ ![]() cos2B+
cos2B+ ![]() .
.
= ![]() sin(2B﹣φ)+
sin(2B﹣φ)+ ![]() ,其中sinφ=
,其中sinφ= ![]() ,cosφ=
,cosφ= ![]() ,∴φ=
,∴φ= ![]() .
.
∴AD2= ![]() sin(2B+A﹣
sin(2B+A﹣ ![]() )+
)+ ![]() =﹣
=﹣ ![]() cos(2B+A)+
cos(2B+A)+ ![]() .
.
∵0<B<π﹣A,
∴A<2B+A<2π﹣A.
∵sinA= ![]() ,∴A
,∴A ![]() ,
,
∴当2B+A=π时,AD2取得最大值 ![]() =
= ![]() =16,
=16,
当2B+A=A或2π﹣A时,AD2取得最小值﹣ ![]() ×
× ![]() +
+ ![]() =1.
=1.
∴1<AD≤4.
所以答案是(1,4].
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() ,以及对余弦定理的定义的理解,了解余弦定理:
,以及对余弦定理的定义的理解,了解余弦定理:![]() ;
;![]() ;
;![]() .
.

练习册系列答案
相关题目