题目内容
在△ABC中,设角A、B、C的对边分别为a、b、c,若a=(cosC,2a-c),b=(b,-cosB)且a⊥b,则B=________.

由a⊥b,
得a·b=bcosC-(2a-c)cosB=0.
利用正弦定理,可得
sinBcosC-(2sinA-sinC)cosB=sinBcosC+cosBsinC-2sinAcosB=0,
即sin(B+C)=sinA=2sinAcosB.
因为sinA≠0,故cosB=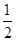 ,因此B=
,因此B= .
.
得a·b=bcosC-(2a-c)cosB=0.
利用正弦定理,可得
sinBcosC-(2sinA-sinC)cosB=sinBcosC+cosBsinC-2sinAcosB=0,
即sin(B+C)=sinA=2sinAcosB.
因为sinA≠0,故cosB=
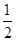 ,因此B=
,因此B= .
.
练习册系列答案
相关题目
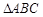 中,
中,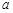 、
、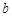 、
、 分别为角
分别为角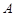 、
、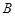 、
、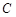 所对的边,若
所对的边,若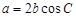 ,则此三角形一定是_______三角形.
,则此三角形一定是_______三角形.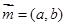 ,
,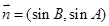 ,
,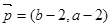 .
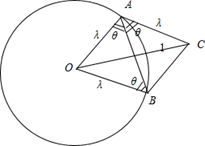
.
 //
// ,求证:ΔABC为等腰三角形;
,求证:ΔABC为等腰三角形;  ,边长
,边长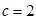 ,角
,角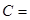
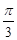 ,求ΔABC的面积 .
,求ΔABC的面积 .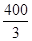 m
m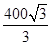 m
m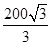 m
m 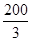 m
m 是三内角对应的三边,已知
是三内角对应的三边,已知 .(1)求角A的大小;(2)若
.(1)求角A的大小;(2)若 =
= ,且△ABC的面积为
,且△ABC的面积为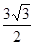 ,求
,求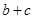 的值.
的值.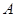 、
、 、
、 、
、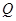 ,欲测量
,欲测量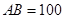 米,如图,同时也能测量出
米,如图,同时也能测量出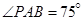 ,
, ,
,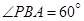 ,
, ,则
,则
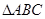 中,内角
中,内角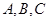 所对的边分别是
所对的边分别是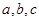 .已知
.已知 ,
,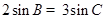 ,则
,则 的值为_______.
的值为_______.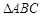 中,
中, ,
,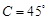 ,
,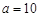 ,则边
,则边 的长为
的长为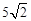
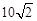

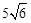
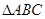 中,角
中,角 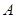 ,
,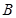 ,
,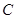 的对边分别为
的对边分别为 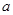 ,
,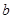 ,
,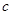 ,且
,且 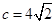 ,
,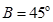 ,面积
,面积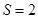 ,则
,则 _________.
_________.