题目内容
20.f(x)=$\left\{\begin{array}{l}{x,x∈[0,1]}\\{2-x,x∈(1,2]}\end{array}\right.$的定义域为[0,2],值域为[0,1].分析 该函数为分段函数,从解析式中即可看出定义域为[0,2],然后在每段里,根据一次函数的单调性求f(x)的范围,然后对求得的f(x)的范围求并集即为原函数的值域.
解答 解:定义域已给出,为:[0,2];
①0≤x≤1时,f(x)=x;
∴0≤f(x)≤1;
②1<x≤2时,f(x)=2-x;
∴f(2)≤f(x)<f(1);
即0≤f(x)≤1;
∴f(x)的值域为[0,1].
故答案为:[0,2],[0,1].
点评 考查函数定义域、值域的概念,分段函数的定义域、值域的求法:在每段里求,再求并集,以及一次函数的单调性.

练习册系列答案
 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
11.函数y=3x2+ax+4在区间[-1,1]上不是单调函数,则实数a的取值范围是( )
| A. | (-6,6) | B. | [-6,6] | C. | (-∞,-6]∪[6,+∞) | D. | (-∞,-6)∪(6,+∞) |
 ,若存在实数
,若存在实数 ,使得
,使得 ,则
,则 的取值范围为( )
的取值范围为( ) B.
B.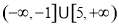
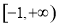 D.
D.