题目内容
10.已知函数f(x)=$\frac{1}{2}$(ax-a-x),(a>0,a≠1)(1)求f(x)的反函数f-1(x);
(2)证明f-1(x)的图象关于原点成中心对称.
分析 (1)利用反函数的定义得出即ax=y$+\sqrt{{y}^{2}+1}$,两边取对数即可.
(2)根据f-1(-x)=loga(-x+$\sqrt{{x}^{2}+1}$),利用奇函数的定义判断即可.
解答 解:(1)∵函数f(x)=$\frac{1}{2}$(ax-a-x),(a>0,a≠1)
∴y=$\frac{1}{2}$(ax-a-x),(a>0,a≠1)
即ax=y$+\sqrt{{y}^{2}+1}$,
x=loga(y$+\sqrt{{y}^{2}+1}$),
∴f(x)的反函数f-1(x)=loga(x+$\sqrt{{x}^{2}+1}$).
(2)定义域为;(-∞,+∞),关于原点对称.
f-1(-x)=loga(-x+$\sqrt{{x}^{2}+1}$)=loga$\frac{1}{\sqrt{{x}^{2}+1}+x}$=-loga($\sqrt{{x}^{2}+1}+x$)=-f-1(x)
∴f-1(x)为奇函数
∴f-1(x)的图象关于原点成中心对称;
点评 本题考查了反函数的定义,奇函数的对称问题,属于容易题,关键是确定解析式,定义域..

练习册系列答案
相关题目
 中,角
中,角 的对边分别为
的对边分别为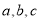 ,且三角形的面积为
,且三角形的面积为 .
. 的大小;
的大小; ,求
,求 的值.
的值. 的一条切线的斜率为
的一条切线的斜率为 ,则切点的横坐标为( )
,则切点的横坐标为( )