题目内容
已知函数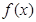 满足
满足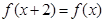 ,当
,当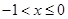 时
时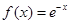 ;当
;当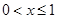 时
时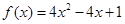 .
.
(Ⅰ)求函数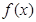 在(-1,1)上的单调区间;
在(-1,1)上的单调区间;
(Ⅱ)若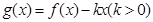 ,求函数
,求函数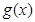 在
在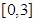 上的零点个数.
上的零点个数.
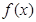 满足
满足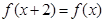 ,当
,当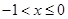 时
时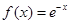 ;当
;当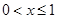 时
时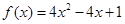 .
.(Ⅰ)求函数
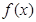 在(-1,1)上的单调区间;
在(-1,1)上的单调区间;(Ⅱ)若
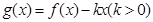 ,求函数
,求函数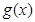 在
在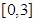 上的零点个数.
上的零点个数.(Ⅰ) 单调递减区间为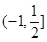 ,递增区间为
,递增区间为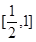 ; (Ⅱ)参考解析
; (Ⅱ)参考解析
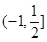 ,递增区间为
,递增区间为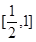 ; (Ⅱ)参考解析
; (Ⅱ)参考解析试题分析:(Ⅰ)因为
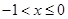 时,函数
时,函数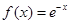 是单调递减的,
是单调递减的,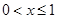 时,函数
时,函数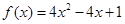 的图像的对称轴是
的图像的对称轴是 ,开口向上.所以
,开口向上.所以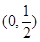 递减,
递减,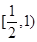 的递增.又因为当
的递增.又因为当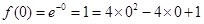 .所以综上可得函数的单调递减区间为
.所以综上可得函数的单调递减区间为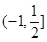 ,递增区间为
,递增区间为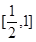 .
.(Ⅱ)因为函数
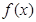 满足
满足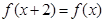 即函数的周期为2.又因为由(Ⅰ)可知(-1,1)的函数走向.所以可以知道函数在[0,3]上的图像走向.因为
即函数的周期为2.又因为由(Ⅰ)可知(-1,1)的函数走向.所以可以知道函数在[0,3]上的图像走向.因为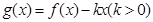 ,求函数
,求函数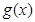 在
在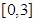 上的零点个数.即等价于求方程
上的零点个数.即等价于求方程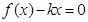 的根的个数.即等价于
的根的个数.即等价于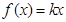 .即等价于函数
.即等价于函数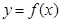 与
与 的图像的交点个数.所以通过如图所示即可解得结论.
的图像的交点个数.所以通过如图所示即可解得结论.试题解析:(1)由题可知
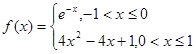
由图可知,函数
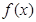 在
在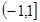 的单调递减区间为
的单调递减区间为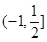 ,
,在
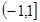 递增区间为
递增区间为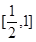 6分
6分考察数形结合思想

(2)当
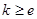 时,
时,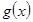 有1个零点 8分
有1个零点 8分当
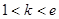 时,
时,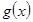 有2个零点 10分
有2个零点 10分当
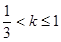 时,
时,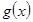 有3个零点 12分
有3个零点 12分当
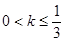 时,
时,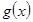 有4个零点 13分
有4个零点 13分
练习册系列答案
相关题目
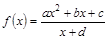 (其中
(其中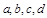 是实数常数,
是实数常数,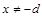 )
)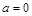 ,函数
,函数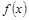 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求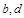 的值;
的值;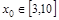 ,总有
,总有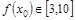 ,求
,求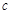 的取值范围;
的取值范围;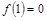 ,
,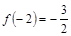 ,且对任意
,且对任意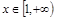 时,不等式
时,不等式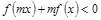 恒成立,求负实数
恒成立,求负实数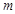 的取值范围.
的取值范围.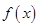 的自变量的取值区间为A,若其值域区间也为A,则称A为
的自变量的取值区间为A,若其值域区间也为A,则称A为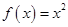 形如
形如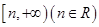 的保值区间;
的保值区间;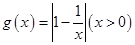 是否存在形如
是否存在形如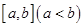 的保值区间?若存在,求出实数
的保值区间?若存在,求出实数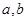 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.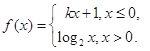 下列是关于函数
下列是关于函数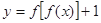 的零点个数的4个判断:
的零点个数的4个判断: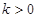 时,有3个零点;②当
时,有3个零点;②当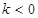 时,有2个零点;
时,有2个零点;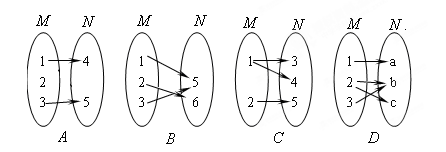
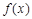 满足
满足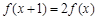 ,且当
,且当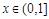 时,
时,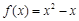 ,则当
,则当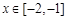 时,
时,
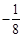
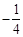

 的值域是
的值域是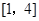 ,则
,则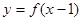 的值域是
的值域是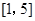

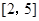
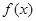 是定义在
是定义在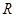 上的函数,并满足
上的函数,并满足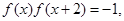 当
当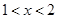 时,
时,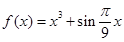 ,则
,则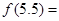 ( )
( )