题目内容
设函数f(θ)=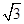 sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
(1)若点P的坐标为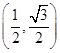 ,求f(θ)的值;
,求f(θ)的值;
(2)若点P(x,y)为平面区域Ω: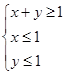 ,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
(1)2;(2)0≤θ≤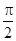 ; f(θ)的最大值等于2 ,f(θ)最小值等于1.
; f(θ)的最大值等于2 ,f(θ)最小值等于1.
解析试题分析:(1)由任意角三角函数的定义可得sinθ,cosθ,代入函数f(θ)=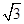 sinθ+cosθ,从而求出f(θ)的值.
sinθ+cosθ,从而求出f(θ)的值.
(2)作出平面区域Ω(即三角区域ABC),如图所示,其点P在该平面区域内,连结OP,便可得角θ的范围.将f(θ)化一得: f(θ)=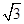 sinθ+cosθ=2sin(θ+
sinθ+cosθ=2sin(θ+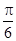 ).根据角θ的范围,结合正弦函数的图象的性质,便 可得f(θ)的范围.
).根据角θ的范围,结合正弦函数的图象的性质,便 可得f(θ)的范围.
试题解析:(1)由点P的坐标和三角函数的定义可得sinθ=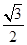 ,cosθ=
,cosθ=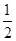 .
.
于是f(θ)=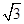 sinθ+cos θ=
sinθ+cos θ=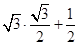 =2.
=2.
(2)作出平面区域Ω(即三角区域ABC)如图所示,其中A(1,0),B(1,1),C(0,1).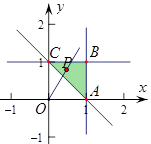
由图可得:0≤θ≤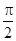 .
.
又f(θ)=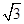 sinθ+cosθ=2sin(θ+
sinθ+cosθ=2sin(θ+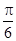 ),且
),且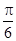 ≤θ+
≤θ+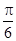 ≤
≤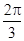 ,
,
故当θ+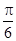 =
=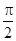 ,即θ=
,即θ=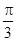 时,f(θ)取得最大值,且最大值等于2 ;
时,f(θ)取得最大值,且最大值等于2 ;
当θ+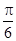 =
=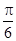 ,即θ=0时,f(θ)取得最小值,且最小值等于1.
,即θ=0时,f(θ)取得最小值,且最小值等于1.
考点:1、任意角三角函数的定义;2、二元不等式组表示的平面区域;3、三角函数的最值.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
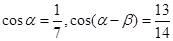 ,且
,且 .
. ;
;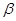 .
.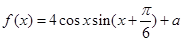 的最大值为2.
的最大值为2.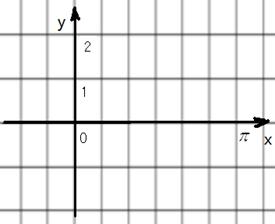
 的值及
的值及 的最小正周期;
的最小正周期;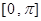 上的图像.
上的图像.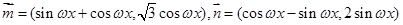 ,其中
,其中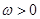 ,若函数
,若函数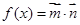 ,且函数
,且函数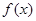 的图象与直线
的图象与直线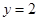 相邻两公共点间的距离为
相邻两公共点间的距离为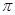 .
.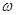 的值;
的值; 中.
中. 分别是
分别是 的对边,且
的对边,且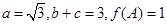 ,求
,求 .
. 的最小正周期;
的最小正周期; 中,
中,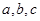 分别是
分别是 A、
A、 ,
, ,
, ,求
,求 的值.
的值.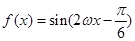 的图象关于直线
的图象关于直线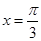 对称,其中
对称,其中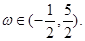
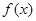 的解析式;
的解析式;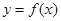 的图象向左平移
的图象向左平移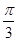 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到 的图象;若函数
的图象;若函数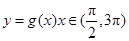 的图象与
的图象与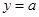 的图象有三个交点且交点的横坐标成等比数列,求
的图象有三个交点且交点的横坐标成等比数列,求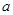 的值.
的值. ,将函数
,将函数 在区间
在区间 内的全部极值点按从小到大的顺序排成数列
内的全部极值点按从小到大的顺序排成数列
 .
. ,数列
,数列 的前
的前 项和为
项和为 ,求
,求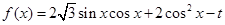 .
.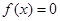 在
在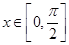 上有解,求
上有解,求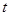 的取值范围;
的取值范围;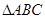 中,
中,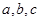 分别是A,B,C所对的边,若
分别是A,B,C所对的边,若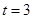 ,且
,且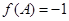 ,
,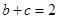 ,求
,求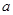 的最小值.
的最小值.