题目内容
在⊿ABC中,角A,B,C的对边分别为A,b,C,且满足(2A-C)CosB=bCosC.
(Ⅰ)求角B的大小;
(Ⅱ)已知函数f(A,C)=Cos2A+sin2C,求f(A,C)的最大值。
(Ⅰ)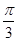 ;(Ⅱ)1+
;(Ⅱ)1+ .
.
解析试题分析:(1)利用正弦定理,结合A、B的范围求出求角B的大小;(Ⅱ)把C用A来表示,在 =1时取最大值.
=1时取最大值.
试题解析:(Ⅰ)∵ (2A-C)CosB=bCosC ∴ 由正弦定理得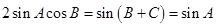
又∵  ∴
∴
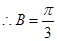
(Ⅱ) 
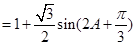

考点:1、正弦定理的应用;2、三角函数的最值.

练习册系列答案
相关题目
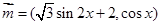 ,
,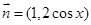 ,设函数
,设函数 ,
, .
. 的最小正周期与最大值;
的最小正周期与最大值;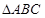 中,
中, 分别是角
分别是角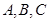 的对边,若
的对边,若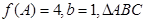 的面积为
的面积为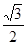 ,求
,求 的值.
的值.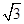 sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.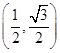 ,求f(θ)的值;
,求f(θ)的值;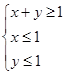 ,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.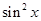 -sin(2x-
-sin(2x- ).
).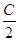 )=
)=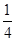 ,若
,若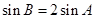 ,求△ABC的面积.
,求△ABC的面积. 的最大值为
的最大值为 ,最小值为
,最小值为 ,其中
,其中 .
. 表示);
表示); 的顶点与平面直角坐标系
的顶点与平面直角坐标系 中的原点
中的原点 重合,始边与
重合,始边与 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点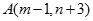 .求
.求 的值.
的值. 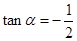 ,求
,求 的值;
的值;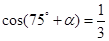 ,且
,且 ,求
,求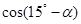 的值.
的值. 中,
中,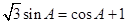 .
. 的大小;
的大小; 的取值范围.
的取值范围.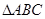 中,角
中,角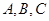 所对的边分别为
所对的边分别为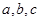 ,且
,且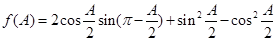 .
.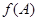 的最大值;
的最大值;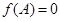 ,
,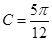 ,
,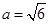 ,求
,求 的值.
的值.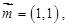 向量
向量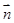 与向量
与向量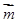 的夹角为
的夹角为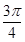 ,且
,且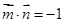 .
.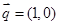 共线,向量
共线,向量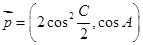 ,其中
,其中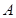 、
、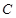 为
为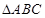 的内角,且
的内角,且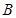 、
、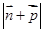 的取值范围.
的取值范围.