题目内容
设 ,将函数
,将函数 在区间
在区间 内的全部极值点按从小到大的顺序排成数列
内的全部极值点按从小到大的顺序排成数列
 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,求
,求 .
.
(1)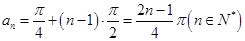 ;(2)
;(2) .
.
解析试题分析:(1)先根据三角函数的恒等变换化简 ,得
,得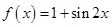 ,再根据三角函数的性质找到极值点,利用等差数列的性质写出数列
,再根据三角函数的性质找到极值点,利用等差数列的性质写出数列 的通项公式;(2)先根据(1)中的结果写出
的通项公式;(2)先根据(1)中的结果写出 的通项公式,然后写出
的通项公式,然后写出 的解析式,在构造出
的解析式,在构造出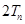 ,利用错位相减法求
,利用错位相减法求 ,计算量比较大,要细心.
,计算量比较大,要细心.
试题解析:(1) ,其极值点为
,其极值点为 , 2分
, 2分
它在 内的全部极值点构成以
内的全部极值点构成以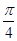 为首项,
为首项,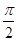 为公差的等差数列, 4分
为公差的等差数列, 4分
所以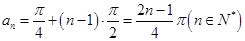 ; 6分
; 6分
(2) , 8分
, 8分
所以 ,
, ,
,
相减,得 ,
,
所以 . 12分
. 12分
考点:1、三角函数的恒等变换及化简;2、三角函数的性质的应用;3、等差数列的通项公式;4、错位相减法求数列的前 项和;5、等比数列的前
项和;5、等比数列的前 项和.
项和.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
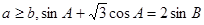 .
.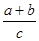 的最大值.
的最大值. .
. 的值;
的值;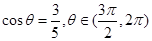 ,求
,求 .
.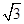 sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.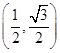 ,求f(θ)的值;
,求f(θ)的值;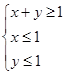 ,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
,上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.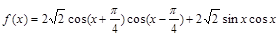
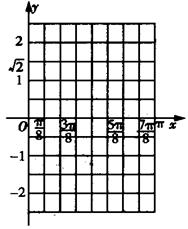
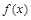 的最小正周期和最大值;
的最小正周期和最大值;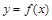 在
在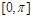 上的图像.
上的图像.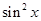 -sin(2x-
-sin(2x- ).
).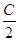 )=
)=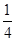 ,若
,若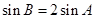 ,求△ABC的面积.
,求△ABC的面积. 的最大值为
的最大值为 ,最小值为
,最小值为 ,其中
,其中 .
. 表示);
表示); 的顶点与平面直角坐标系
的顶点与平面直角坐标系 中的原点
中的原点 重合,始边与
重合,始边与 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点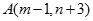 .求
.求 的值.
的值.  中,
中,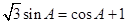 .
. 的大小;
的大小; 的取值范围.
的取值范围.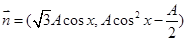 ,
,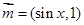 ,
,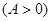 ,函数
,函数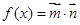 的最大值为
的最大值为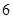 .
.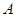 ;
;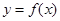 的图像向左平移
的图像向左平移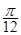 个单位,再将所得图像上各点的横坐标缩短为原来的
个单位,再将所得图像上各点的横坐标缩短为原来的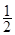 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数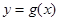 的图像,求
的图像,求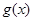 在
在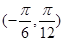 上的值域.
上的值域.