题目内容
若函数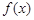 满足:集合
满足:集合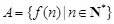 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数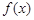 是等比源函数.
是等比源函数.
(1)判断下列函数:①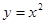 ;②
;②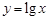 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)
(2)证明:函数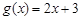 是等比源函数;
是等比源函数;
(3)判断函数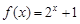 是否为等比源函数,并证明你的结论.
是否为等比源函数,并证明你的结论.
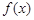 满足:集合
满足:集合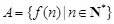 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数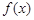 是等比源函数.
是等比源函数.(1)判断下列函数:①
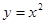 ;②
;②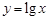 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)(2)证明:函数
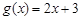 是等比源函数;
是等比源函数;(3)判断函数
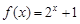 是否为等比源函数,并证明你的结论.
是否为等比源函数,并证明你的结论.(1)①②都是等比源函数;(2)参考解析;(3)参考解析
试题分析:(1)函数
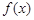 满足:集合
满足:集合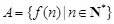 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数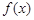 是等比源函数.由等比源函数的定义可知.令x=1,2,4.即可得函数
是等比源函数.由等比源函数的定义可知.令x=1,2,4.即可得函数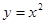 对应的三项为等比数列.令x=10,100,10000即可得函数
对应的三项为等比数列.令x=10,100,10000即可得函数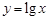 对应的三项成等比数列.所以①②都是等比源函数.
对应的三项成等比数列.所以①②都是等比源函数.(2)由函数
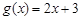 ,通过列举三项即可得到证明.
,通过列举三项即可得到证明.(3)函数
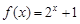 ,不是等比源函数.假设存在三项使得函数
,不是等比源函数.假设存在三项使得函数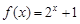 是等比源函数,利用等比数列的等比通项的知识,以及奇偶性的知识即可得到函数
是等比源函数,利用等比数列的等比通项的知识,以及奇偶性的知识即可得到函数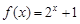 ,不是等比源函数.
,不是等比源函数.试题解析:(1)①②都是等比源函数;4分
(2)证明:
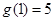 ,
,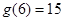 ,
,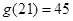
因为
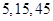 成等比数列
成等比数列所以函数
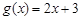 是等比源函数;10分
是等比源函数;10分其他的数据也可以
(3)函数
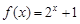 不是等比源函数.证明如下:
不是等比源函数.证明如下:假设存在正整数
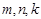 且
且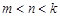 ,使得
,使得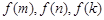 成等比数列,
成等比数列,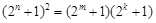 ,整理得
,整理得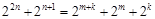 ,
,等式两边同除以
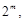 得
得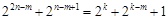 .
.因为
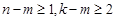 ,所以等式左边为偶数,等式右边为奇数,
,所以等式左边为偶数,等式右边为奇数,所以等式
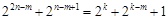 不可能成立,
不可能成立,所以假设不成立,说明函数
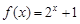 不是等比源函数.18分
不是等比源函数.18分
练习册系列答案
相关题目
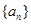 ,其前
,其前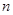 项和
项和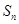 满足
满足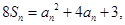 且
且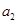 是
是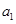 和
和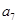 的等比中项.
的等比中项.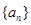 的通项公式;
的通项公式;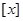 表示不超过实数
表示不超过实数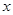 的最大整数,记
的最大整数,记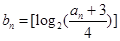 ,求
,求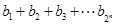 .
.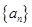 的前
的前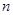 项和为
项和为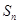 ,已知
,已知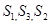 成等差数列,(1)求数列
成等差数列,(1)求数列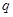 ,(2)若
,(2)若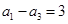 ,求
,求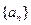 的前n项和为
的前n项和为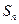 ,若
,若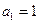 ,
,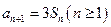 ,则
,则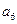 =( )
=( )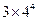
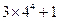
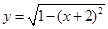 图像上存在不同的三点到原点的距离构成等比数列,则以下
图像上存在不同的三点到原点的距离构成等比数列,则以下
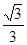
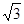
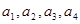 成等比数列,其公比为2,则
成等比数列,其公比为2,则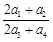 的值为( )
的值为( ) 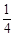
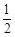
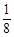
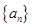 中,
中,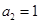 ,
,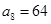 ,则
,则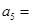 ( )
( )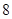
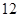
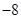
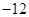
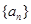 满足:
满足: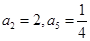 ,则公比q为( )
,则公比q为( )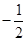
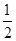
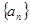 是递增数列,
是递增数列,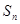 是
是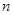 项和.若
项和.若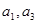 是方程
是方程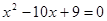 的两个根,则
的两个根,则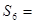 _________ .
_________ .