题目内容
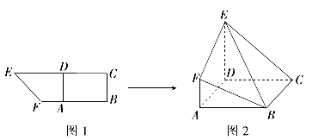
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
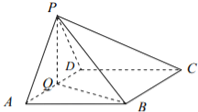
(1)若PA=PD,求证:平面PQB⊥平面PAD;
(2)若平面PAD⊥平面ABCD,且PA=PD=AD=2,点M在线段PC上,且PM=3MC,求三棱锥P﹣QBM的体积.
【答案】(1)详见解析(2)![]()
【解析】
试题分析:(1)由PA=PD,得到PQ⊥AD,又底面ABCD为菱形,∠BAD=60°,得BQ⊥AD,利用线面垂直的判定定理得到AD⊥平面PQB利用面面垂直的判定定理得到平面PQB⊥平面PAD;(2)由平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PQ⊥AD,得PQ⊥平面ABCD,BC平面ABCD,得PQ⊥BC,得BC⊥平面PQB,即得到高,利用椎体体积公式求出
试题解析:(1)∵PA=PD,
∴PQ⊥AD,
又∵底面ABCD为菱形,∠BAD=60°,
∴BQ⊥AD,PQ∩BQ=Q,
∴AD⊥平面PQB
又AD平面PAD,
∴平面PQB⊥平面PAD
(2)∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,
∴PQ⊥平面![]() ,
,![]() 平面
平面![]() ,
,
∴PQ⊥BC
又BC⊥BQ,![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() ,
,
∴![]()

练习册系列答案
相关题目