题目内容
已知函数f(x)=sinx+cosx.
(Ⅰ)若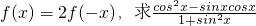 的值;
的值;
(Ⅱ)求函数F(x)=f(x)•f(-x)+f2(x)的最大值和单调递增区间.
解:(Ⅰ)∵f(x)=sinx+cosx,∴f(-x)=cosx-sinx.…(1分)
又∵f(x)=2f(-x),
∴sinx+cosx=2(cosx-sinx)且cosx≠0 .…(3分)
.…(3分)
∴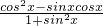 =
=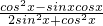 =
=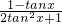 =
=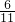 ;…(6分)
;…(6分)
(Ⅱ)由题知F(x)=cos2x-sin2x+1+2sinxcosx?F(x)=cos2x+sin2x+1 …(10分)
…(10分)
∴当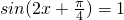 时,
时,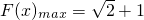 .…(11分)
.…(11分)
由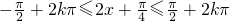 解得,单调递增区间为
解得,单调递增区间为  .…(12分)
.…(12分)
分析:(I)首先得出f(-x)=cosx-sinx,进而化简sinx+cosx=2(cosx-sinx)得出tanx的值,然后将所求式子中的“1”用sin2x+cos2x替换,再分子分母同时除以cos2x,即可求出结果;
(II)先求出F(x)=cos2x+sin2x+1= (2x+
(2x+ )+1,然后就可以求出最大值和单调区间.
)+1,然后就可以求出最大值和单调区间.
点评:此题考查了三角函数的化简求值以及复合函数的单调性,熟练掌握公式是解题的关键,同时注意“1”和sin2x+cos2x的灵活转化,属于中档题.
又∵f(x)=2f(-x),
∴sinx+cosx=2(cosx-sinx)且cosx≠0
 .…(3分)
.…(3分)∴
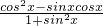 =
=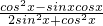 =
=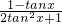 =
=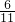 ;…(6分)
;…(6分)(Ⅱ)由题知F(x)=cos2x-sin2x+1+2sinxcosx?F(x)=cos2x+sin2x+1
 …(10分)
…(10分)∴当
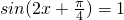 时,
时,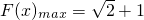 .…(11分)
.…(11分)由
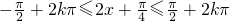 解得,单调递增区间为
解得,单调递增区间为  .…(12分)
.…(12分)分析:(I)首先得出f(-x)=cosx-sinx,进而化简sinx+cosx=2(cosx-sinx)得出tanx的值,然后将所求式子中的“1”用sin2x+cos2x替换,再分子分母同时除以cos2x,即可求出结果;
(II)先求出F(x)=cos2x+sin2x+1=
 (2x+
(2x+ )+1,然后就可以求出最大值和单调区间.
)+1,然后就可以求出最大值和单调区间.点评:此题考查了三角函数的化简求值以及复合函数的单调性,熟练掌握公式是解题的关键,同时注意“1”和sin2x+cos2x的灵活转化,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
