边长为2的正方体挖去一个几何体后的三视图如图所示.则剩余部分的体积是( )A．8-$\frac{2π}{3}$B．8-$\frac{π}{3}$C．8-2πD．$\frac{2π}{3}$ 题目和参考答案——青夏教育精英家教网—

题目内容

6．边长为2的正方体挖去一个几何体后的三视图如图所示，则剩余部分的体积是（　　）

A．

8-$\frac{2π}{3}$

B．

8-$\frac{π}{3}$

C．

8-2π

D．

$\frac{2π}{3}$

分析由已知中的三视图，可得该几何体是一个正方体挖去一个圆锥所得的组合体，分别计算正方体和圆锥的体积，相减可得答案．

解答解：由已知中的三视图，可得该几何体是一个正方体挖去一个圆锥所得的组合体，
正方体的体积为：2×2×2=8，
圆锥的体积为：$\frac{1}{3}$×π×2=$\frac{2π}{3}$，
故组合体的体积V=8-$\frac{2π}{3}$．
故选：A

点评本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．

练习册系列答案

相关题目

16．

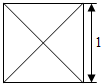已知某几何体的俯视图是如图所示的边长为1的正方形，主视图与左视图是边长为1的正三角形，则其全面积是（　　）

17．

用大小和形状完全相同的小正方体木块搭成一个几何体，使得它的主视图和俯视图如图所示，则搭成这样的一个几何体至少需要小正方体木块的个数为（　　）

14．双曲线x²-y²=1右支上一点P（a，b）到直线l：y=x的距离d=$\sqrt{2}$．则a+b=（　　）

$\frac{1}{2}$或-$\frac{1}{2}$

D．

2或-2

1．若函数f（x）=$\sqrt{2}sin\frac{x}{2}cos\frac{x}{2}-\sqrt{2}{sin^2}\frac{x}{2}$，则函数f（x）的最小正周期为2π；函数f（x）在区间[-π，0]上的最小值是-1-$\frac{\sqrt{2}}{2}$．

11．f（x）=log₃x•log₃（3x）的值域为[-$\frac{1}{4}$，+∞）．

18．设x，y，向量$\overrightarrow a=（x，1），\overrightarrow b=（1，y），\overrightarrow c=（2，-4）$，且$\overrightarrow a⊥\overrightarrow c$，$\overrightarrow b∥\overrightarrow c$，则$|{\overrightarrow a+\overrightarrow b}$|=$\sqrt{10}$．

15．设变量x，y满足约束条件$\left\{\begin{array}{l}{x＞0}\\{y＞0}\\{x+2y-4＜0}\\{x+2y-2＞0}\end{array}\right.$，则目标函数z=x²+y²的取值范围是（$\frac{4}{5}$，16）．

16．某几何体的三视图如图所示，则该几何体的体积可以是（　　）

试题分类