题目内容
16.某几何体的三视图如图所示,则该几何体的体积可以是( )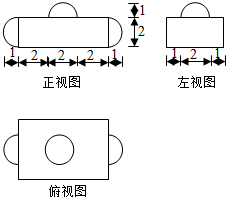
| A. | $48+\frac{4}{3}π$ | B. | 48+2π | C. | $48+\frac{8}{3}π$ | D. | 48+3π |
分析 由已知中的三视图可得该几何体是一个长方体和三个半球的组合体,分别求其体积,相加可得答案.
解答 解:由已知中的三视图可得该几何体是一个长方体和三个半球的组合体,
长方体的长,宽,高,分别为6,4,2,故体积为:48,
半球的半径均为1,故体积为:$\frac{2}{3}π$,
故组合体的体积为:48+$\frac{2}{3}π$×3=48+2π,
故选:B
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
6.边长为2的正方体挖去一个几何体后的三视图如图所示,则剩余部分的体积是( )


| A. | 8-$\frac{2π}{3}$ | B. | 8-$\frac{π}{3}$ | C. | 8-2π | D. | $\frac{2π}{3}$ |
7.某几何体的三视图,如图所示,则该几何体的体积为( )


| A. | 72一$\frac{9π}{2}$ | B. | 72-4π | C. | 72一$\frac{7π}{2}$ | D. | 72-3π |
4. 某几何体的三视图如图所示,则该几何体最长的梭长为( )
某几何体的三视图如图所示,则该几何体最长的梭长为( )
 某几何体的三视图如图所示,则该几何体最长的梭长为( )
某几何体的三视图如图所示,则该几何体最长的梭长为( )| A. | 16 | B. | 5 | C. | $\sqrt{41}$ | D. | 4$\sqrt{2}$ |
11.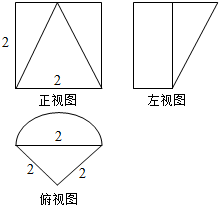 正三棱柱被一个平面截去一部分后与半圆柱组成一个几何体,该几何体的三视图如图所示,则该几何体的表面积为( )
正三棱柱被一个平面截去一部分后与半圆柱组成一个几何体,该几何体的三视图如图所示,则该几何体的表面积为( )
 正三棱柱被一个平面截去一部分后与半圆柱组成一个几何体,该几何体的三视图如图所示,则该几何体的表面积为( )
正三棱柱被一个平面截去一部分后与半圆柱组成一个几何体,该几何体的三视图如图所示,则该几何体的表面积为( )| A. | 3π+4+$\sqrt{3}$+$\sqrt{7}$ | B. | 3π+6+$\sqrt{3}$ | C. | 2π+4+$\sqrt{3}$$+\sqrt{7}$ | D. | 2π+6$+\sqrt{3}$ |
8.函数y=$\sqrt{m{x}^{2}-6mx+m+8}$的定义域是R,则实数m的取值范围是( )
| A. | 0<m≤1 | B. | 0≤m≤1 | C. | 0<m<1 | D. | 0≤m<1 |
5.方程ax2-3x-1=0至少有一个负数根,则实数a的取值范围是( )
| A. | (-∞,-$\frac{9}{4}$) | B. | (-∞,-$\frac{9}{4}$] | C. | [-$\frac{9}{4}$,+∞) | D. | [0,+∞) |
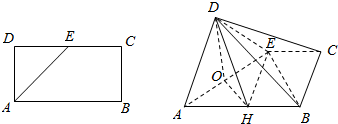 如图所示,在矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=2$\sqrt{3}$,O,H分别为AE,AB的中点,平面BDE∩面DOH=l.
如图所示,在矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=2$\sqrt{3}$,O,H分别为AE,AB的中点,平面BDE∩面DOH=l.