题目内容
【题目】已知曲线![]() 上的点
上的点![]() 与定点
与定点![]() 的距离与它到直线
的距离与它到直线![]() 的距离的比是常数
的距离的比是常数![]() ,又斜率为
,又斜率为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() 。
。
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)若![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)设![]() ,直线
,直线![]() 与曲线
与曲线![]() 的另一个交点为
的另一个交点为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的另一个交点为
的另一个交点为![]() .若
.若![]() 和点
和点![]() 共线,求
共线,求![]() 的值。
的值。
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)2.
;(Ⅲ)2.
【解析】
(Ⅰ)由已知条件点到点的距离与点到线的距离之比是常数,列出关系式,化简求出曲线方程
(Ⅱ)根据题意设直线![]() 的方程为
的方程为![]() ,联立直线方程与曲线方程,运用弦长公式求出弦长表达式,求出最大值
,联立直线方程与曲线方程,运用弦长公式求出弦长表达式,求出最大值
(Ⅲ)设出点坐标,联立直线方程与曲线方程,再由三点共线求出![]() 的值
的值
解:(Ⅰ)根据题意可得: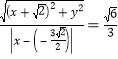
整理得:![]()
故曲线![]() 的方程为
的方程为![]()
(Ⅱ)设直线![]() 的方程为
的方程为![]() ,
,
由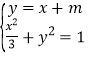 消去
消去![]() 可得
可得![]()
则![]()
设![]() 则
则![]()
则![]()
易得当,![]() ,故
,故![]() 的最大值为
的最大值为![]()
(Ⅲ)设![]()
则![]() ①,
①,![]() ②,
②,
又![]() ,所以可设
,所以可设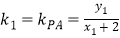 ,直线
,直线![]() 的方程为
的方程为![]()
由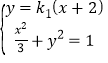 消去
消去![]() 可得
可得![]()
则![]()
即![]()
代入①式可得![]() ,所以
,所以![]()
所以![]() ,同理可得
,同理可得![]()
![]()
因为![]() 三点共线,所以
三点共线,所以![]()
将点![]() 的坐标代入化简可得
的坐标代入化简可得![]() ,即
,即![]() .
.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案【题目】企业需为员工缴纳社会保险,缴费标准是根据职工本人上一年度月平均工资(单位:元)的![]() 缴纳,
缴纳,
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
t | 1 | 2 | 3 | 4 | 5 |
y | 270 | 330 | 390 | 460 | 550 |
某企业员工甲在2014年至2018年各年中每月所撒纳的养老保险数额y(单位:元)与年份序号t的统计如下表:
(1)求出t关于t的线性回归方程![]() ;
;
(2)试预测2019年该员工的月平均工资为多少元?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
(注: ,
,![]() ,其中
,其中![]() )
)
【题目】襄阳市拟在2021年奥体中心落成后申办2026年湖北省省运会,据了解,目前武汉,宜昌,黄石等申办城市因市民担心赛事费用超支而准备相继退出,某机构为调查襄阳市市民对申办省运会的态度,选取某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 60 | ||
年龄大于50岁 | 10 | ||
合计 | 80 | 100 |
(1)根据已知数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过![]() 的前提下认为不同年龄与支持申办省运会无关?
的前提下认为不同年龄与支持申办省运会无关?
附: ![]() ,
, ![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |