题目内容
【题目】已知在△ABC中，角A，B，C所对的边分别为a，b，c，且2S△ABC＝
·
.
(1)求角B的大小；
(2)若b＝2，求a＋c的取值范围.
【答案】见解析
【解析】
解：(1)由已知得acsin B＝
accos B，∴tan B＝，
∵0<B<π，∴B＝
.
(2)法一：由余弦定理得4＝a2＋c2－2accos ，即4＝(a＋c)2－3ac≥(a＋c)2－3
2(当且仅当a＝c时取等号)，解得0<a＋c≤4.
又a＋c>b，∴2<a＋c≤4，∴a＋c的取值范围是(2,4].
法二：由正弦定理得a＝
sin A，c＝sin C，
又A＋C＝
，∴a＋c＝ (sin A＋sin C)＝ [sin A＋sin(A＋B)]＝
＝4
＝4sin
.
∵0<A<，∴
<A＋<
，∴
<sin≤1，∴a＋c的取值范围是(2,4].
天天向上一本好卷系列答案
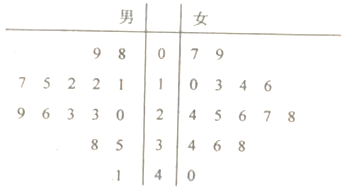
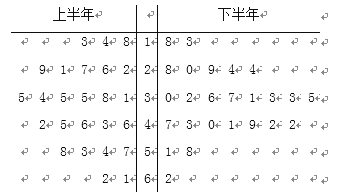
小学生10分钟应用题系列答案【题目】某工厂于2016年下半年对生产工艺进行了改造（每半年为一个生产周期），从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本，用茎叶图表示（如图）．已知每个生产周期内与其中位数误差在±5范围内（含±5）的产品为优质品，与中位数误差在±15范围内（含±15）的产品为合格品（不包括优质品），与中位数误差超过±15的产品为次品．企业生产一件优质品可获利润20元，生产一件合格品可获利润10元，生产一件次品要亏损10元
（Ⅰ）求该企业2016年一年生产一件产品的利润为10的概率；
（Ⅱ）是否有95%的把握认为“优质品与生产工艺改造有关”．
附：
P（K2≥k） | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2=
．
【题目】为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下列表：
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全班50人中随机抽取1人，抽到喜爱打篮球的学生的概率为
．
（1）请将上表补充完整（不用写计算过程）；
（2）能否有99.5％的把握认为喜爱打篮球与性别有关？说明你的理由．
下面的临界值表供参考：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式：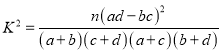 
，其中
）