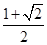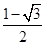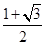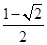题目内容
设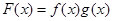 是
是 上的奇函数,当
上的奇函数,当 时,
时, ,且
,且 ,则不等式
,则不等式 的解集是( )
的解集是( )
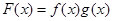 是
是 上的奇函数,当
上的奇函数,当 时,
时, ,且
,且 ,则不等式
,则不等式 的解集是( )
的解集是( )A. | B. |
C. | D. |
A
解:因 f′(x)g(x)+f(x)g′(x)>0,
即[f(x)g(x)]'>0故F(x)在x<0时递增,
又∵F(x)=f(x)g(x)是R上的奇函数,∴F(x)的图象关于原点对称,
所以F(x)在x>0时也是增函数.∵f(2)g(2)=0,∴f(-2)g(-2)=0.
即F(-2)=0且F(2)=0所以F(x)>0的解集为:x<-2或0<x<2.
即[f(x)g(x)]'>0故F(x)在x<0时递增,
又∵F(x)=f(x)g(x)是R上的奇函数,∴F(x)的图象关于原点对称,
所以F(x)在x>0时也是增函数.∵f(2)g(2)=0,∴f(-2)g(-2)=0.
即F(-2)=0且F(2)=0所以F(x)>0的解集为:x<-2或0<x<2.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
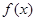 满足满足
满足满足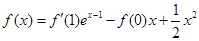 ;
;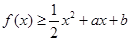 ,求
,求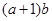 的最大值.
的最大值.



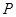 (元)与时间
(元)与时间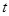 (天)所组成的有序数对
(天)所组成的有序数对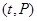 落在下图中的两条线段上,该股票在30天内的日交易量
落在下图中的两条线段上,该股票在30天内的日交易量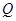 (万股)与时间
(万股)与时间
 (万元)表示该股票日交易额,写出
(万元)表示该股票日交易额,写出 万元建起一座汽车零件加工厂,第一年各种经费
万元建起一座汽车零件加工厂,第一年各种经费 万元,以后每年增加
万元,以后每年增加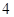 万元,每年的产品销售收入
万元,每年的产品销售收入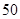 万元.
万元.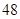 万元出售该厂;
万元出售该厂;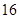 万元出售该厂.
万元出售该厂.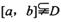 和常数c,使得对任意x1
和常数c,使得对任意x1 ,都有
,都有 ,且对任意x2
,且对任意x2 D,当
D,当 时,
时, 恒成立,则称函数f(x)为区间D上的“平顶型”函数.给出下列说法:
恒成立,则称函数f(x)为区间D上的“平顶型”函数.给出下列说法: 为R上的“平顶型”函数;
为R上的“平顶型”函数; 时,函数,
时,函数, 是区间
是区间 上的“平顶型”函数.
上的“平顶型”函数.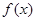 对任意实数
对任意实数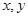 满足:
满足: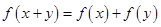 ,且
,且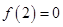 ,则下列结论正确的是_____________.
,则下列结论正确的是_____________.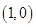 对称;④
对称;④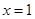 对称.
对称. 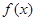 是定义域为R,又
是定义域为R,又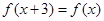 ,当
,当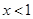 时,
时,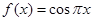
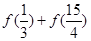 值为( )
值为( )