题目内容
(本小题满分13分)
已知首项不为零的数列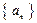 的前
的前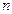 项和为
项和为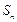 ,若对任意的
,若对任意的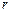 ,
,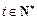 ,都有
,都有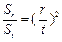 .
.
(Ⅰ)判断数列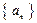 是否为等差数列,并证明你的结论;
是否为等差数列,并证明你的结论;
(Ⅱ)若数列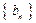 的第
的第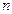 项
项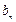 是数列
是数列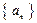 的第
的第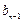 项
项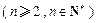 ,且
,且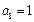 ,
,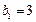 ,求数列
,求数列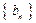 的前
的前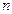 项和
项和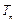 .
.
已知首项不为零的数列
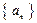 的前
的前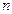 项和为
项和为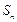 ,若对任意的
,若对任意的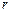 ,
,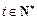 ,都有
,都有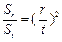 .
.(Ⅰ)判断数列
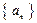 是否为等差数列,并证明你的结论;
是否为等差数列,并证明你的结论;(Ⅱ)若数列
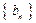 的第
的第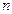 项
项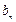 是数列
是数列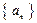 的第
的第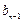 项
项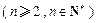 ,且
,且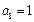 ,
,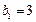 ,求数列
,求数列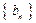 的前
的前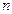 项和
项和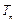 .
.(1)是(2)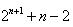
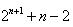
(Ⅰ)令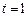 ,
, ,得
,得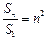 ,于是
,于是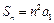 . ……
. ……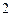 分
分
当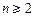 时,
时,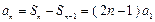 ;
;
当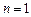 时,
时,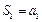 也适合上式.
也适合上式.
综上知,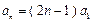 . ……
. ……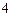 分
分
所以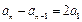 .
.
故数列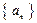 是公差
是公差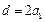 的等差数列. ……
的等差数列. …… 分
分
(Ⅱ)当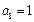 时,由(Ⅰ)知,
时,由(Ⅰ)知,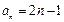 .
.
于是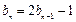 ,即
,即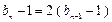 .
.
因此数列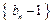 是首项为
是首项为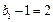 ,公比为
,公比为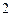 的等比数列,所以
的等比数列,所以
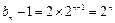 .即
.即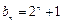 . ……
. ……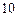 分
分
故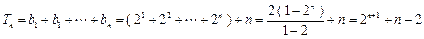 .
.
……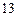 分
分
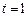 ,
, ,得
,得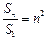 ,于是
,于是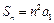 . ……
. ……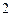 分
分当
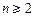 时,
时,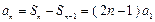 ;
;当
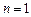 时,
时,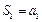 也适合上式.
也适合上式.综上知,
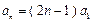 . ……
. ……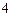 分
分所以
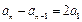 .
.故数列
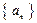 是公差
是公差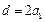 的等差数列. ……
的等差数列. ……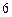 分
分(Ⅱ)当
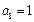 时,由(Ⅰ)知,
时,由(Ⅰ)知,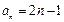 .
.于是
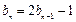 ,即
,即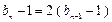 .
.因此数列
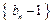 是首项为
是首项为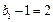 ,公比为
,公比为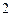 的等比数列,所以
的等比数列,所以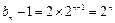 .即
.即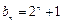 . ……
. ……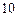 分
分故
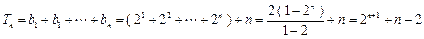 .
.……
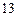 分
分
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
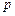 ,
,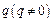 是实数,方程
是实数,方程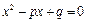 有两个实根
有两个实根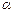 ,
,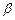 ,数列
,数列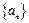 满足
满足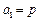 ,
,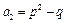 ,
,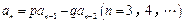
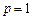 ,
,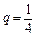 ,求
,求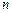 项和.
项和.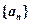 、
、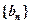 的前n项和分别为
的前n项和分别为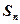 、
、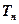 ,
,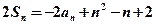 ,
,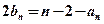 .
.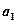 、
、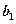 的值,并证明数列
的值,并证明数列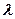 的值,使数列
的值,使数列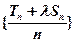 是等差数列.
是等差数列.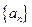 的前n项和为
的前n项和为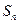 ,若对任意的r、s
,若对任意的r、s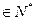 ,都有
,都有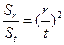 .
.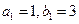 ,数列
,数列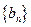 的第n项是数列
的第n项是数列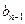 项
项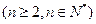 ,求
,求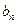 ;
;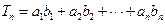 .
.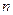 边形的内角的度数成等差数列,若公差是
边形的内角的度数成等差数列,若公差是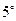 ,且最大角是
,且最大角是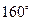 ,则
,则
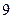
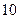
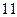
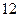
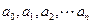 成等差数列,则有等式
成等差数列,则有等式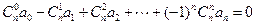 成立,类比上述性质,相应地:若
成立,类比上述性质,相应地:若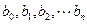 成等比数列,则有等式__ _成立。
成等比数列,则有等式__ _成立。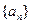 的递推公式
的递推公式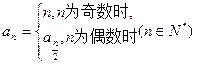 求出这个数列各项的值,使得这个数列中的每一项都是奇数。则
求出这个数列各项的值,使得这个数列中的每一项都是奇数。则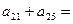 ;
;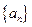 和
和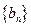 的前
的前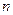 项和分别为
项和分别为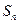 和
和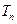 ,且
,且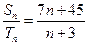 ,则使得
,则使得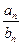 为整数的正整数
为整数的正整数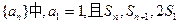 成等差数列
成等差数列 ,则
,则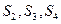 分别为 ,由此猜想出
分别为 ,由此猜想出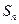 = 。
= 。