题目内容
(本小题满分14分)
如图,棱柱ABCD—![]() 的所有棱长都为2,
的所有棱长都为2, ![]() ,侧棱
,侧棱![]() 与底面ABCD的所成角为60°,
与底面ABCD的所成角为60°,![]() ⊥平面ABCD,
⊥平面ABCD,![]() 为
为![]() 的中点.
的中点.
(Ⅰ)证明:BD⊥![]() ;
;
(Ⅱ)证明:![]() 平面
平面![]() ;
;
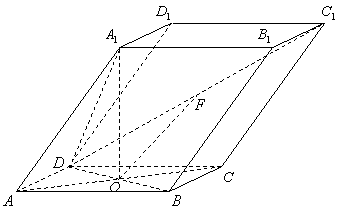 (Ⅲ)求二面角D
(Ⅲ)求二面角D![]()
![]()
![]() C的余弦值.
C的余弦值.
【解析】(I)![]() 棱柱ABCD—
棱柱ABCD—![]() 的所有棱长都为2,
的所有棱长都为2,
![]() 四边形ABCD为菱形,
四边形ABCD为菱形,![]() . .......................................1分
. .......................................1分
又![]() ⊥平面ABCD,
⊥平面ABCD, ![]() 平面ABCD,
平面ABCD,
![]() . ..................................2分
. ..................................2分
又![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() , .......................3分
, .......................3分
![]() 平面
平面![]() ,
,
![]() BD⊥
BD⊥![]() . .......................................4分
. .......................................4分
(Ⅱ)连结![]()
![]() 四边形ABCD为菱形,
四边形ABCD为菱形,![]()
![]() 是
是![]() 的中点. .............................. 5分
的中点. .............................. 5分
又![]() 点F为
点F为![]() 的中点,
的中点,
![]() 在
在![]() 中,
中,![]() , ................................6分
, ................................6分
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]()
![]() 平面
平面![]() .......................8分
.......................8分
(III)以![]() 为坐标系的原点,分别以
为坐标系的原点,分别以![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系. ![]() 侧棱
侧棱![]() 与底面ABCD的所成角为60°,
与底面ABCD的所成角为60°,![]() ⊥平面ABCD.
⊥平面ABCD.
![]() ,在
,在![]() 中,可得
中,可得![]()
在![]() 中,
中,![]() .
.
得![]() ......................10分
......................10分
设平面![]() 的法向量为
的法向量为![]()
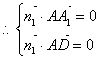
![]()
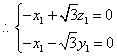
可设![]() ..............................11分
..............................11分
又![]()
![]() 平面
平面![]()
所以,平面![]() 的法向量为
的法向量为![]() .............................12分
.............................12分
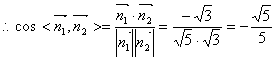 ,
,
![]() 二面角D—
二面角D—![]() —C为锐角,
—C为锐角,
故二面角D—![]() —C的余弦值是
—C的余弦值是![]() . ...........................14分
. ...........................14分

 春雨教育同步作文系列答案
春雨教育同步作文系列答案 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)