题目内容
（2011•顺义区二模）已知函数f(x)=2sinxcosx+
cos2x，x∈R
（1）求函数f（x）（2）的最小正周期；
（2）求f（x）在区间上的最小值及f（x）取最小值时x的值．
| 3 |
（1）求函数f（x）（2）的最小正周期；
（2）求f（x）在区间上的最小值及f（x）取最小值时x的值．
分析：（1）利用二倍角公式，平方关系，两角和的正弦函数，化简函数y=sin2x+2sinxcosx+3cos2x，为一个角的一个三角函数的形式，然后利用三角函数的周期公式求出最小正周期，
（2）先求出整体角的范围，然后利用三角函数的有界性求出三角函数的最大值、最小值．
（2）先求出整体角的范围，然后利用三角函数的有界性求出三角函数的最大值、最小值．
解答：解：（1）f(x)=2sinxcosx+
cos2x=sin2x+
cos2x=2(
sin2x+
cos2x)=2sin(2x+
)…（5分）
所以函数f（x）的最小正周期为π． …（6分）
（2）由-
≤x≤
得0≤2x+
≤
，…．（9分）
所以当2x+
=
π时，即x=
时，函数f（x）取得最小值，且最小值为 -
故函数f（x）在区间[-
，
]上的最小值为-
，此时x=
．…．（13分）
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
所以函数f（x）的最小正周期为π． …（6分）
（2）由-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| 4π |
| 3 |
所以当2x+
| π |
| 3 |
| 4 |
| 3 |
| π |
| 2 |
| 3 |
故函数f（x）在区间[-
| π |
| 6 |
| π |
| 2 |
| 3 |
| π |
| 2 |
点评：本题主要考查三角函数的最小正周期的求法．一般先将原函数化简为：y=Asin（ωx+φ）的形式．
练习册系列答案
相关题目
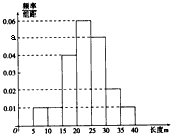（2011•顺义区二模）某棉纺厂为了解一批棉花的质量，从中随机抽测100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标）．所得数据均在区间[5，40]中，其频率分布直方图如图所示，由图中数据可知a=