题目内容
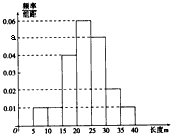 (2011•顺义区二模)某棉纺厂为了解一批棉花的质量,从中随机抽测100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中,其频率分布直方图如图所示,由图中数据可知a=
(2011•顺义区二模)某棉纺厂为了解一批棉花的质量,从中随机抽测100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中,其频率分布直方图如图所示,由图中数据可知a=0.05
0.05
,在抽测的100根中,棉花纤维的长度在[20,30]内的有55
55
根.分析:根据各组的累积频率为1,结合频率=组距×矩形的高,构造关于a的方程,解方程可得a值;纤维长度在[20,30]内的概率,即纤维长度在[20,30]内的各组频率的累加值,利用频率=组距×矩形的高,频数=频率×样本容量,可得答案.
解答:解:∵各组的累积频率为1,
∴(3×0.01+0.02+0.04+0.06+a)×5=1
故a=0.05
棉花纤维的长度在区间[20,30]内的频率为5×(0.06+0.05)=0.55,
亦即棉花纤维的长度在此区间内的频率为0.55,
所以,这批棉花的纤维的长度在[20,30)内的概率为0.55.
故棉花纤维的长度在[20,30)内的有100×0.55=55根
故答案为:0.05,55
∴(3×0.01+0.02+0.04+0.06+a)×5=1
故a=0.05
棉花纤维的长度在区间[20,30]内的频率为5×(0.06+0.05)=0.55,
亦即棉花纤维的长度在此区间内的频率为0.55,
所以,这批棉花的纤维的长度在[20,30)内的概率为0.55.
故棉花纤维的长度在[20,30)内的有100×0.55=55根
故答案为:0.05,55
点评:本题考查频率分布直方图的知识.考查读图的能力,读图时要全面细致,同时,解题方法要灵活多样,切忌死记硬背,要充分运用数形结合思想来解决由统计图形式给出的数学实际问题.

练习册系列答案
相关题目