题目内容
（2011•顺义区二模）已知
=(1，0)，
=(0，1)，
=2
+
，
=λ
-
，当
∥
时，实数λ等于（ ）
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| a |
| b |
分析：先根据条件求出向量
与向量
的坐标，然后根据
∥
则x1y2-x2y1=0建立等式，解之即可．
| a |
| b |
| a |
| b |
解答：解：∵
=(1，0)，
=(0，1)，
=2
+
，
=λ
-
，
∴
=2（1，0）+（0，1）=（2，1），
=λ（1，0）-（0，1）=（λ，-1）
∵
∥
∴2×（-1）-1×λ=0解得λ=-2
故选D．
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
∴
| a |
| b |
∵
| a |
| b |
∴2×（-1）-1×λ=0解得λ=-2
故选D．
点评：本题主要考查了平面向量共线（平行）的坐标表示，同时考查了向量的加减法的运算，属于基础题．
练习册系列答案
相关题目
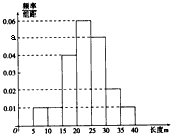（2011•顺义区二模）某棉纺厂为了解一批棉花的质量，从中随机抽测100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标）．所得数据均在区间[5，40]中，其频率分布直方图如图所示，由图中数据可知a=