题目内容
已知二次函数f(x)＝x2－bx＋c，f(0)＝4，f(1＋x)＝f(1－x)，则( )
| A．f(bx)≥f(cx) | B．f(bx)≤f(cx) |
| C．f(bx)>f(cx) | D．f(bx)<f(cx) |
B
由f(0)＝4，得c＝4，由f(1＋x)＝f(1－x)，知二次函数f(x)图象的对称轴为x＝1，即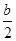
＝1，即b＝2，故f(x)＝x2－2x＋4，bx＝2x，cx＝4x. 当x≥0时，cx≥bx≥1，而二次函数f(x)在(1，＋∞)上单调递增，故f(bx)≤f(cx)；当x<0时，0<cx<bx<1，而二次函数f(x)在(－∞，1)上单调递减，故f(bx)<f(cx)．综上可知选B.
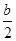＝1，即b＝2，故f(x)＝x2－2x＋4，bx＝2x，cx＝4x. 当x≥0时，cx≥bx≥1，而二次函数f(x)在(1，＋∞)上单调递增，故f(bx)≤f(cx)；当x<0时，0<cx<bx<1，而二次函数f(x)在(－∞，1)上单调递减，故f(bx)<f(cx)．综上可知选B.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
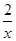且f(4)＝
.
.
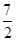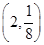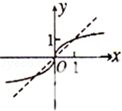
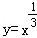的图象是（ ）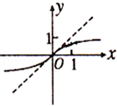
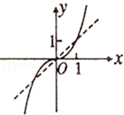
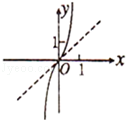
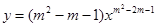在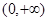
上是增函数，则 
=_________．
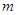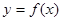的图像过点
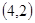，则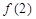
= ．
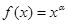的部分对应值如下表：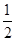
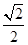
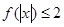的解集是( )．
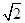≤x≤