题目内容
【题目】如图，有一块半圆形空地，开发商计划建一个矩形游泳池ABCD及其矩形附属设施EFGH，并将剩余空地进行绿化，园林局要求绿化面积应最大化．其中半圆的圆心为O，半径为R，矩形的一边AB在直径上，点C、D、G、H在圆周上，E、F在边CD上，且
，设
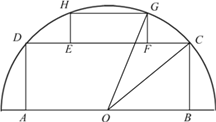
（1）记游泳池及其附属设施的占地面积为
，求
的表达式；
（2）当
为何值时，能符合园林局的要求？
【答案】（1）
；（2）当
满足
时，符合园林局要求.
【解析】试题分析：（1）由圆的性质可得， 
， 
，由
为等边三角形，
可得， 
， 
，所以
，结合三角形面积公式可得结果 ；（2）由
可得极值点
满足， 
，利用导数研究函数的单调性可得当
时
是单调减函数，当
时， 
是单调增函数，所以当
时， 
取得最小值.
试题解析：（1）由题意， 
， 
，且
为等边三角形，
所以， 
， 
，
， 
．
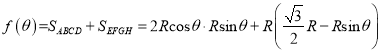
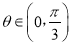（2）要符合园林局的要求，只要
最小，
由（1）知， 
令
，即
，解得
或
（舍去），
令
.
当
时， 
是单调减函数，当
时， 
是单调增函数，所以当
时， 
取得最小值.
答：当
满足
时，符合园林局要求.
思路点睛】本题主要考查阅读能力、数学建模能力和化归思想以及导数在解决实际问题中的应用，属于难题. 与实际应用相结合的题型也是高考命题的动向，这类问题的特点是通过现实生活的事例考查书本知识，解决这类问题的关键是耐心读题、仔细理解题，只有吃透题意，才能将实际问题转化为数学模型进行解答.理解本题题意的关键是：将游泳池及其附属设施的占地面积为关于
的函数，然后利用导数解答.
练习册系列答案
全能测控一本好卷系列答案
相关题目
