题目内容
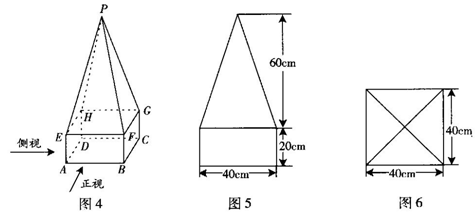
如图:三棱柱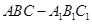 中,
中,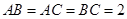 ,
, ,侧棱
,侧棱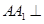 底面
底面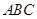 ,
,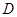 为
为 的中点,
的中点, 为
为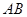 边上的动点。
边上的动点。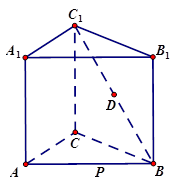
(1)若 为
为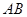 中点,求证:
中点,求证: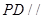 平面
平面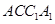
(2)若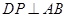 ,求四棱锥
,求四棱锥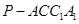 的体积。
的体积。
(1)连接 ,得
,得 ,进一步得到
,进一步得到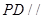 平面
平面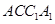 。
。
(2)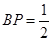 ,
,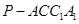 的体积为
的体积为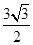
解析试题分析:(1)若 为
为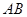 中点,连接
中点,连接 ,则DP是三角形
,则DP是三角形 的中位线,即
的中位线,即 ,又
,又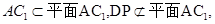 所以,
所以,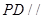 平面
平面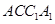 。
。
(2)若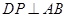 ,在平面
,在平面 内,作
内,作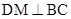 ,因为 , 三棱柱
,因为 , 三棱柱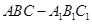 中,
中,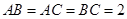 ,
,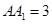 ,侧棱
,侧棱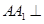 底面
底面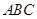 ,所以,M是BC的中点,
,所以,M是BC的中点,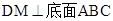 ,连MP知,
,连MP知,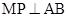 ,
,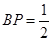 ,所以,P到平面
,所以,P到平面 的距离,即P到AC的距离
的距离,即P到AC的距离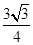 ,故四棱锥
,故四棱锥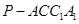 的体积为
的体积为
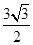 。
。
考点:正三棱柱的几何特征,平行关系,垂直关系,体积计算。
点评:中档题,立体几何问题中,平行关系、垂直关系,角、距离、面积、体积等的计算,是常见题型,基本思路是将空间问题转化成为平面问题,利用平面几何知识加以解决。要注意遵循“一作,二证,三计算”。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
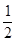 CD=2,点M在线段EC上.
CD=2,点M在线段EC上.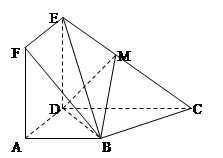
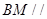 面
面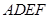 ;
;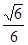 时,求三棱锥M-BDE的体积.
时,求三棱锥M-BDE的体积.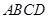 中,
中,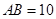 ,
,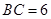 ,将矩形沿对角线
,将矩形沿对角线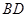 把
把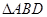 折起,使
折起,使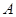 移到
移到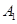 点,且
点,且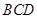 上的射影
上的射影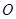 恰好在
恰好在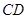 上.
上.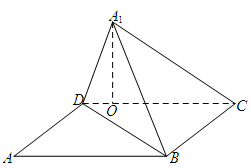
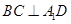 ;
; 平面
平面 ;
;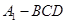 的体积.
的体积. ,在直角梯形
,在直角梯形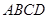 中,
中,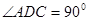 ,
,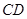 ∥
∥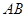 ,
, ,
,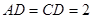 ,将
,将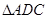 沿
沿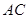 折起,使平面
折起,使平面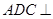 平面
平面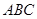 ,得到几何体
,得到几何体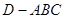 ,如图2所示.
,如图2所示.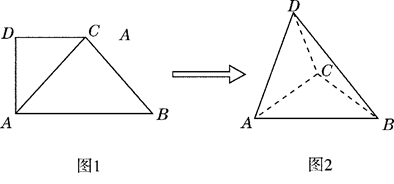
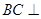 平面
平面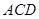 ;
;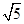 .
.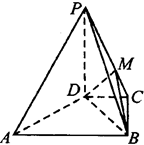
 是边长为2的正方形,
是边长为2的正方形, ⊥平面
⊥平面 ,
, //
// 且
且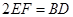 .
.
 ⊥平面
⊥平面 ;
; 的体积.
的体积. 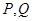 在正视图中所示位置:
在正视图中所示位置: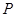 为所在线段中点,
为所在线段中点,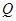 为顶点,求在几何体表面上,从
为顶点,求在几何体表面上,从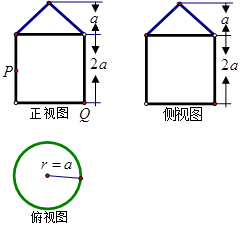
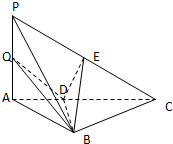
 平面PEG.
平面PEG.