题目内容
11.已知x>0,y>0,x+2y-2xy+8=0,求xy的最小值.分析 首先分析题目由已知x>0,y>0,x+2y-2xy=8,求xy的最小值,猜想到基本不等式的用法,利用a+b≥2$\sqrt{ab}$在代入已知条件,化简为不等式,解不等式求最值.
解答 解:考察基本不等式x+2y=x•(2y)-8
≥2$\sqrt{2xy}$(当且仅当x=2y时取等号),
整理得xy-$\sqrt{2}$$\sqrt{xy}$-4≥0,
即($\sqrt{xy}$-2$\sqrt{2}$)($\sqrt{xy}$+$\sqrt{2}$)≥0,
由$\sqrt{xy}$>0,即有$\sqrt{xy}$≥2$\sqrt{2}$.
所以xy≥8(当且仅当x=2y=4时取等号)
则xy的最小值是8.
点评 此题主要考查基本不等式的用法,对于不等式a+b≥2$\sqrt{ab}$在求最大值最小值的问题中应用非常广泛,需要同学们多加注意.

练习册系列答案
相关题目
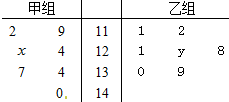 右边茎叶图记录了甲、乙两组各7名学生在一次数学测试中的成(单位:分).已知甲组数据的众数为124,乙组数据的平均数即为甲组数据的中位数,则x、y的值分别为( )
右边茎叶图记录了甲、乙两组各7名学生在一次数学测试中的成(单位:分).已知甲组数据的众数为124,乙组数据的平均数即为甲组数据的中位数,则x、y的值分别为( )