题目内容
已知函数y=2cos(
x-
),x∈[-π,π].
(1)求函数的单调区间;
(2)求函数的最小值及取得最小值时x的值.
| 1 |
| 2 |
| π |
| 3 |
(1)求函数的单调区间;
(2)求函数的最小值及取得最小值时x的值.
考点:余弦函数的单调性,三角函数的最值
专题:三角函数的图像与性质
分析:(1)由x∈[-π,π],可求出
x-
∈[-
,
],由余弦函数的图象和性质可求函数的单调区间;
(2)由余弦函数的图象和性质可求函数的最小值及取得最小值时x的值.
| 1 |
| 2 |
| π |
| 3 |
| 5π |
| 6 |
| π |
| 6 |
(2)由余弦函数的图象和性质可求函数的最小值及取得最小值时x的值.
解答:
解:(1)∵x∈[-π,π].
∴
x-
∈[-
,
]
∴由余弦函数的图象和性质可知,其单调递增区间为:[-
,0],单调递减区间为:[0,
].
(2)由余弦函数的图象和性质可知,当x=-π时,ymin=2cos[(
×(-π)-
]=-1.
∴
| 1 |
| 2 |
| π |
| 3 |
| 5π |
| 6 |
| π |
| 6 |
∴由余弦函数的图象和性质可知,其单调递增区间为:[-
| 5π |
| 6 |
| π |
| 6 |
(2)由余弦函数的图象和性质可知,当x=-π时,ymin=2cos[(
| 1 |
| 2 |
| π |
| 3 |
点评:本题主要考察了余弦函数的单调性,三角函数的最值,属于基本知识的考查.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
若a=ln2,b=ln3,c=lg0.1,则a,b,c的大小顺序是( )
| A、a>b>c |
| B、c>b>a |
| C、b>a>c |
| D、b>c>a |
函数f(x)=
,则f(1)+f(-3)的值是( )
|
| A、-1 | B、1 | C、-2 | D、2 |
已知sin(
+α)=
,则cosα的值是( )
| π |
| 2 |
| 3 |
| 5 |
A、-
| ||
B、±
| ||
C、
| ||
D、
|
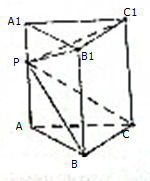 如图所示,点P为三棱柱ABC-A1B1C1侧棱AA1上一动点,若四棱锥P-BCC1B1的体积为V,则三棱柱ABC-A1B1C1的体积为( )
如图所示,点P为三棱柱ABC-A1B1C1侧棱AA1上一动点,若四棱锥P-BCC1B1的体积为V,则三棱柱ABC-A1B1C1的体积为( )| A、2V | ||
| B、3V | ||
C、
| ||
D、
|
y=x2-3x+2在∈[
,3]上的最小值与最大值分别为( )
| 1 |
| 2 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|