题目内容

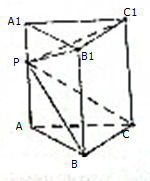如图所示，点P为三棱柱ABC-A1B1C1侧棱AA1上一动点，若四棱锥P-BCC1B1的体积为V，则三棱柱ABC-A1B1C1的体积为（　　）
A、2V
B、3V
C、
4V
3
D、
3V
2
考点：棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：利用AA1到对面距离不变，转化P到A点，利用棱锥与棱柱的体积关系，即可得出结论．
解答： 解：由题意，借款合同是棱柱，所以AA1到对面距离不变，移动P到A点，由棱锥的体积的推导方法可知：
VP-BCC1B1=
2
3
VABC-A1B1C1．∴VABC-A1B1C1=
3
2
V．
故选：D．
点评：本题考查棱柱、棱锥、棱台的体积，考查学生的计算能力，基本知识的考查．
练习册系列答案
相关题目
在等差数列{an}中，已知a1+a2=4，a2+a3=8，则a7等于（　　）
A、7B、10C、13D、19
（1）已知角θ的终边上有一点P（x，-1）（x≠0），且tanθ=-x，求sinθ，cosθ；
（2）已知函数f（x）=
1-sin(x-
3π
2
)+cos(x+
π
2
)+tan
3
4
π
cosx
，设tanα=-
4
3
，求f（α）的值．
设A={x∈N|1≤x＜6}，则下列正确的是（　　）
A、6∈AB、0∈A
C、3?AD、3.5∉a
已知函数y=2cos（
1
2
x-
π
3
），x∈[-π，π]．
（1）求函数的单调区间；
（2）求函数的最小值及取得最小值时x的值．
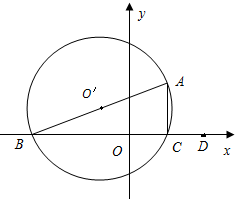如图，在平面直角坐标系中，△ABC内接于⊙O，其中AB为⊙O直径，A（1，3），B（-3，0），C（1，0）．
（1）请在x轴上找一点D，使得△BDA与△BAC相似（不包含全等），并求出点D的坐标；
（2）在（1）的条件下，如果P，Q分别是BA，BD上的动点，连接PQ，设BP=DQ=m．问是否存在这样的m，使得△BPQ与△BDA相似？若存在，求出m的值；若不存在，请说明理由．
△ABC中，角A、B、C所对应的边分别为a，b，c，若
a-c
sinB-sinC
=
b
sinA+sinB

（1）求角A；
（2）若函数f（x）=cos2（x+A）-sin2（x-A）+
1
2
cosx，x∈[A，π]，求函数f（x）的值域．
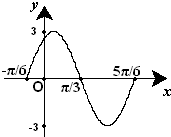已知函数f（x）=Asin（ωx+φ） （A＞0，ω＞0，|φ|＜π）的一段图象（如图）所示．
（1）求函数的解析式；
（2）写出这个函数的单调增区间；
（3）若x∈[-
π
6
，
π
3
]时，函数g（x）=f（x）+m的最小值为2，试求出函数g（x）的最大值并求出此时x的取值．
已知抛物线y2=-8x的焦点为F1，准线与x轴的交点为F2，直线l：x-y+4=0，以F1、F2为焦点的椭圆C过直线l上一点．
（1）求长轴最短时椭圆C的方程；
（2）在（1）中的椭圆上存在四点M、N、P、Q满足：
PF2
∥
F2Q
，
MF2
∥
F2N
，
PF2
⊥
F2M
，求四边形PMQN的面积的最大值和最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网