题目内容
若函数f（x）=ax3-bx+4，当x=2时，函数f（x）有极值为-
，
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若f（x）=k有3个解，求实数k的取值范围．
| 4 |
| 3 |
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若f（x）=k有3个解，求实数k的取值范围．
（Ⅰ）f′（x）=3ax2-b
由题意；
，解得
，
∴所求的解析式为f(x)=
x3-4x+4
（Ⅱ）由（1）可得f′（x）=x2-4=（x-2）（x+2）
令f′（x）=0，得x=2或x=-2，
∴当x＜-2时，f′（x）＞0，当-2＜x＜2时，f′（x）＜0，当x＞2时，f′（x）＞0
因此，当x=-2时，f（x）有极大值
，
当x=2时，f（x）有极小值-
，
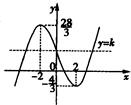
∴函数f(x)=
x3-4x+4的图象大致如图．
由图可知：-
＜k＜
．
由题意；
|
|
∴所求的解析式为f(x)=
| 1 |
| 3 |
（Ⅱ）由（1）可得f′（x）=x2-4=（x-2）（x+2）
令f′（x）=0，得x=2或x=-2，
∴当x＜-2时，f′（x）＞0，当-2＜x＜2时，f′（x）＜0，当x＞2时，f′（x）＞0
因此，当x=-2时，f（x）有极大值
| 28 |
| 3 |
当x=2时，f（x）有极小值-
| 4 |
| 3 |
∴函数f(x)=
| 1 |
| 3 |
由图可知：-
| 4 |
| 3 |
| 28 |
| 3 |
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
