题目内容
已知函数f（x）=
x3+
（b-1）x2+cx．
（1）当b=-3，c=3时，求f（x）的极值；
（2）若f（x）在（-∞，x1），（x2，+∞）上递增，在（x1，x2）上递减，x2-x1＞1，求证：b2＞2（b+2c）；
（3）在（2）的条件下，若t＜x1，试比较t2+bt+c与x1的大小．
| 1 |
| 3 |
| 1 |
| 2 |
（1）当b=-3，c=3时，求f（x）的极值；
（2）若f（x）在（-∞，x1），（x2，+∞）上递增，在（x1，x2）上递减，x2-x1＞1，求证：b2＞2（b+2c）；
（3）在（2）的条件下，若t＜x1，试比较t2+bt+c与x1的大小．
f′（x）=x2+（b-1）x+c
（1）b=-3，c=3时，f′（x）=x2-4x+3=（x-1）（x-3）
根据导数的知识可得，y极大=f(1)=
，y极小=f(3)=0
（2）f'（x）=x2+（b-1）x+c
由题意可得x1，x2为x2+（b-1）x+c=0的两根，而|x1-x2|=x2-x1=
＞1从而可证
（3）由于x2+（b-1）x+c=（x-x1）（x-x2），则可得t2+bt+c=（t-x1）（t-x2）+t，t2+bt+c-x1=（t-x1）（t-x2）+t-x1=（t-x1）（t-x2+1），结合已知可证（t-x1）（t-x2+1）＞0，即证
（1）b=-3，c=3时，f′（x）=x2-4x+3=（x-1）（x-3）
根据导数的知识可得，y极大=f(1)=
| 4 |
| 3 |
（2）f'（x）=x2+（b-1）x+c
由题意可得x1，x2为x2+（b-1）x+c=0的两根，而|x1-x2|=x2-x1=
| (b-1)2-4c |
（3）由于x2+（b-1）x+c=（x-x1）（x-x2），则可得t2+bt+c=（t-x1）（t-x2）+t，t2+bt+c-x1=（t-x1）（t-x2）+t-x1=（t-x1）（t-x2+1），结合已知可证（t-x1）（t-x2+1）＞0，即证
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
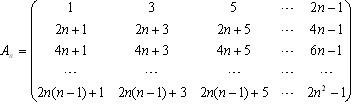任取An中的一个元素，记为x1；划去x1所在的行和列，将剩下的元素按原来的位置关系组成n-1阶方阵An-1，任取An-1中的一个元素，记为x2；划去x2所在的行和列，…；将最后剩下的一个元素记为xn，记Sn=x1+x2+…+xn，则