题目内容
【题目】已知函数f(x)= ![]() 满足:f(1)=1,f(﹣2)=4.
满足:f(1)=1,f(﹣2)=4.
(1)求a,b的值,并探究是否存在常数c,使得对函数f(x)在定义域内的任意x,都有f(x)+f(c﹣x)=4成立;
(2)当x∈[1,2]时,不等式f(x)≤ ![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】
(1)解:由 ![]() ,得
,得 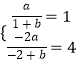 ,解得
,解得 ![]() .
.
∴ ![]() (x≠﹣1).
(x≠﹣1).
方法1:假设存在常数c符合要求,即f(x)+f(c﹣x)=4,x≠﹣1成立.
特别当x=0时有f(0)+f(c)=4,即 ![]() ,解得c=﹣2.
,解得c=﹣2.
下面证明f(x)+f(﹣2﹣x)=4,x≠﹣1恒成立.事实上,当x≠﹣1时,
则f(x)+f(﹣2﹣x)= ![]() =
= ![]() .
.
∴存在常数c=﹣2,满足题设要求;
方法2:假设存在常数c符合要求,即f(x)+f(c﹣x)=4,x≠﹣1成立.
则 ![]() ,
,
即 ![]() ,
,
变形得,﹣x2+(c﹣1)x+c=﹣x2+(c﹣1)x+2(c+1),
整理得,c=﹣2.
∴存在常数c=﹣2,满足题设要求
(2)解:不等式f(x)≤ ![]() 即为
即为 ![]()
![]() 对x∈[1,2]恒成立,
对x∈[1,2]恒成立,
即 ![]() 对x∈[1,2]恒成立,
对x∈[1,2]恒成立,
故必有0<m<1或m>2
在0<m<1或m>2下,问题化为 ![]() 对x∈[1,2]恒成立,
对x∈[1,2]恒成立,
即mx﹣m≤x2≤mx+m对x∈[1,2]恒成立,
①当x=1时, ![]() 或m>2.
或m>2.
②当x≠1时, ![]() 且
且 ![]() 对x∈[1,2]恒成立,
对x∈[1,2]恒成立,
对于 ![]() 对x∈[1,2]恒成立,等价于
对x∈[1,2]恒成立,等价于 ![]() ,
,
令t=x+1,x∈[1,2],则x=t﹣1,t∈(2,3],
![]() ,t∈(2,3]递增,
,t∈(2,3]递增,
∴ ![]() ,
,
即 ![]() ,结合0<m<1或m>2,
,结合0<m<1或m>2,
∴m>2.
对于 ![]() 对x∈[1,2]恒成立,等价于
对x∈[1,2]恒成立,等价于 ![]() ,
,
令t=x﹣1,x∈[1,2],则x=t+1,t∈(0,1],
![]() ,t∈(0,1]递减,
,t∈(0,1]递减,
∴ ![]() ,
,
∴m≤4,结合0<m<1或m>2,
∴0<m<1或2<m≤4,
综上,实数m的取值范围为2<m≤4
【解析】(1)由 ![]() ,得
,得 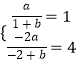 ,解得a,b的值, 方法1:假设存在常数c符合要求,即f(x)+f(c﹣x)=4,x≠﹣1成立,特别当x=0时,解得c的值,然后证明
,解得a,b的值, 方法1:假设存在常数c符合要求,即f(x)+f(c﹣x)=4,x≠﹣1成立,特别当x=0时,解得c的值,然后证明
f(x)+f(﹣2﹣x)=4,x≠﹣1恒成立,当x≠﹣1时,则f(x)+f(﹣2﹣x)=4,故存在常数c=﹣2,满足题设要求;
方法2:假设存在常数c符合要求,即f(x)+f(c﹣x)=4,x≠﹣1成立,则 ![]() ,变形得,﹣x2+(c﹣1)x+c=﹣x2+(c﹣1)x+2(c+1),整理得c的值,故存在常数c=﹣2,满足题设要求;(2)不等式f(x)≤
,变形得,﹣x2+(c﹣1)x+c=﹣x2+(c﹣1)x+2(c+1),整理得c的值,故存在常数c=﹣2,满足题设要求;(2)不等式f(x)≤ ![]() 即为
即为 ![]()
![]() 对x∈[1,2]恒成立,即
对x∈[1,2]恒成立,即 ![]() 对x∈[1,2]恒成立,则0<m<1或m>2,进一步化为
对x∈[1,2]恒成立,则0<m<1或m>2,进一步化为 ![]() 对x∈[1,2]恒成立,即mx﹣m≤x2≤mx+m对x∈[1,2]恒成立,再分类讨论①当x=1时,
对x∈[1,2]恒成立,即mx﹣m≤x2≤mx+m对x∈[1,2]恒成立,再分类讨论①当x=1时, ![]() 或m>2,②当x≠1时,求出0<m<1或2<m≤4,综上,实数m的取值范围可求.
或m>2,②当x≠1时,求出0<m<1或2<m≤4,综上,实数m的取值范围可求.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案