题目内容
【题目】设集合A=R,集合B={y|y>0},下列对应关系中是从集合A到集合B的映射的是( )
A.x→y=|x|
B.x→y= ![]()
C.![]()
D.![]()
【答案】C
【解析】解:∵|0|=0,而 0R+ , 集合A中的元素0在集合B中没有像,故选项A 不是映射.
对于选项B,集合A中的元素1在集合B中没有像,故选项B不是映射.
对于选项C,集合A中的所有元素在集合B中都有唯一的像和它对应,故选项C是映射.
对于选项D,由于函数的定义域不是R,故选项D不是映射.
故选 C.
【考点精析】掌握映射的相关定义是解答本题的根本,需要知道对于映射f:A→B来说,则应满足:(1)集合A中的每一个元素,在集合B中都有象,并且象是唯一的;(2)集合A中不同的元素,在集合B中对应的象可以是同一个;(3)不要求集合B中的每一个元素在集合A中都有原象;注意:映射是针对自然界中的所有事物而言的,而函数仅仅是针对数字来说的.所以函数是映射,而映射不一定的函数.

练习册系列答案
相关题目
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在下图中的两条线段上,该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示. 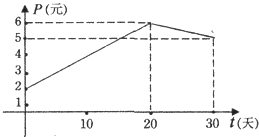
第t天 | 4 | 10 | 16 | 22 |
Q(万股) | 36 | 30 | 24 | 18 |
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)在(2)的结论下,用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几日交易额最大,最大值为多少?