题目内容
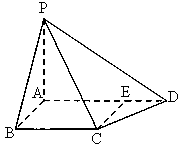
(本题满分12分)如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,CE∥AB。
(Ⅰ)求证:CE⊥平面PAD;
(Ⅱ)若PA=AB=1,AD=3,且CD与平面PAD所成的角为45°,求二面角B—PE—A的正切值。
【答案】

 DE=CE=AB=1,AE=2, (6分)连PE,BE
DE=CE=AB=1,AE=2, (6分)连PE,BE
法一:以A为原点O,AD为OX轴,AB为OY轴,AP为OZ轴建立空间直角坐标系
A(0,0,0),B(0,1,0)E(2,0,0)
由(I)知AB为平面PAE的法向量且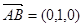 设平面PBE的法向量为
设平面PBE的法向量为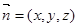
由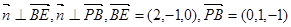
得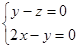 解之,得
解之,得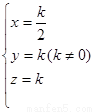 取
取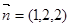 (8分)
(8分)
设所求二面角的平面角为 ,则
,则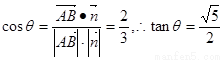 (12分)
(12分)
法二:作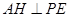 于H,连BH,由(I)知
于H,连BH,由(I)知 平面AHB
平面AHB
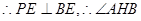 为所求二面角的平面角 (10分)
为所求二面角的平面角 (10分)
在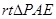 中,
中,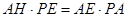 由,得
由,得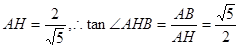 (12分)
(12分)
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得.  ,
, 为
为 的中点.
的中点.
 时,求平面
时,求平面 为何值时,在棱
为何值时,在棱 上存在点
上存在点 ,使
,使 平面
平面 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱 ,为
,为 中点,
中点, 为
为 中点,
中点, 为
为 上一个动点.
上一个动点.
 ;
; 的平
的平
 中,已知
中,已知 的直径
的直径 的中点.
的中点.
 所成角的正弦值.
所成角的正弦值.
