题目内容
(本题满分12分)如图,在四棱锥P—ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=2,E是PB的中点,F是AD的中点.

⑴求异面直线PD与AE所成角的大小;
⑵求证:EF⊥平面PBC ;
⑶求二面角F—PC—B的大小..
【答案】
(Ⅰ)连结BD ∵PD⊥平面ABCD,
∴平面PDB⊥平面ABCD,
过点E作EO⊥BD于O,连结AO.
则EO∥PD,且EO⊥平面ABCD
.∴∠AEO为异面直线PD,AE所成的角…………3分
∵E是PB的中点,则O是BD的中点,且EO=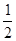 PD=1.
PD=1.
在Rt△EOA中,AO=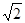 ,
,
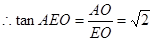 .
.
即异面直线PD与AE所成角的大小为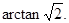 …………………………… 4分
…………………………… 4分
(Ⅱ)连结FO, ∵F是AD的中点, ∴OF⊥AD.∵EO⊥平面ABCD,
由三垂线定理,得EF⊥AD.又∵AD∥BC,∴EF⊥BC. ………………… 6分
连结FB.可求得FB = PF =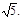 则EF⊥PB.又∵PB∩BC
= B,∴EF⊥平面PBC. …………………8分
则EF⊥PB.又∵PB∩BC
= B,∴EF⊥平面PBC. …………………8分
(Ⅲ)取PC的中点G,连结EG,FG.则EG是FG在平面PBC内的射影
∵PD⊥平面ABCD, ∴PD⊥BC又DC⊥BC,且PD∩DC = D,
∴BC⊥平面PDC,∴BC⊥PC,∵EG∥BC,则EG⊥PC∴FG⊥PC
∴∠FGE是二面角F—PC—B的平面角 ………………………………………10分
在Rt△FEG中,EG=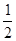 BC
= 1,GF =
BC
= 1,GF = 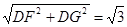 ,
,
 ∴二面角F—PC—B的大小为
∴二面角F—PC—B的大小为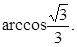 …12分
…12分
说明:如学生用向量法解题,则建立坐标系给写出相关点的坐标给2分,第(1)问正确给
2分,第(2)问正确给4分,第(3)问正确给4分。
【解析】略

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得.  ,
, 为
为 的中点.
的中点.
 时,求平面
时,求平面 为何值时,在棱
为何值时,在棱 上存在点
上存在点 ,使
,使 平面
平面 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱 ,为
,为 中点,
中点, 为
为 中点,
中点, 为
为 上一个动点.
上一个动点.
 ;
; 的平
的平 中,已知
中,已知 的直径
的直径 的中点.
的中点.
 所成角的正弦值.
所成角的正弦值.
