题目内容
【题目】已知点A(2,0),点B(﹣2,0),直线l:(λ+3)x+(λ﹣1)y﹣4λ=0(其中λ∈R).
(1)求直线l所经过的定点P的坐标;
(2)若直线l与线段AB有公共点,求λ的取值范围;
(3)若分别过A,B且斜率为 ![]() 的两条平行直线截直线l所得线段的长为4
的两条平行直线截直线l所得线段的长为4 ![]() ,求直线l的方程.
,求直线l的方程.
【答案】
(1)解:由题意,(λ+3)x+(λ﹣1)y﹣4λ=0(其中λ∈R),
则λ(x+y﹣4)+(3x﹣y)=0,
∵λ∈R,
∴ ![]() ,
,
解的 ![]() ,
,
∴直线l所经过的定点P的坐标(1,3)
(2)解:∵点A(2,0),点B(﹣2,0),定点P的坐标(1,3);
∴kPA= ![]() =﹣3,kPB=
=﹣3,kPB= ![]() =1,
=1,
∵直线l与线段AB有公共点,
当λ=1时,直线x=1,与线段AB有公共点,
当λ≠1时,直线l的斜率k= ![]() ,
,
∴ ![]() ≥1或
≥1或 ![]() ≤﹣3,
≤﹣3,
解的﹣1≤λ<1,或1<λ≤3,
综上所述:λ的取值范围为[﹣1,3]
(3)解:分别过A,B且斜率为 ![]() 的两条平行直线,分别为y=
的两条平行直线,分别为y= ![]() x+2
x+2 ![]() ,y=
,y= ![]() x﹣2
x﹣2 ![]() ,
,
由(1)知,l恒过点(1,3),
当斜率存在时,设直线l为y﹣3=k(x﹣1),由图象易知,直线l的倾斜角为30°,即k= ![]() ,
,
∴过点p的直线l为y﹣3= ![]() (x﹣1),即
(x﹣1),即 ![]() x﹣3y+9﹣
x﹣3y+9﹣ ![]() =0.
=0.
当直线l的斜率不存在时,由(1)可知直线过定点(1,3),则直线方程为x=1,
令x=1,可知y1=3 ![]() ,y2=﹣
,y2=﹣ ![]() ,|y1﹣y2|=4
,|y1﹣y2|=4 ![]() ,符合题意,
,符合题意,
综上所述:直线l的方程为x=1或 ![]() x﹣3y+9﹣
x﹣3y+9﹣ ![]() =0
=0
【解析】(1)由题意,(λ+3)x+(λ﹣1)y﹣4λ=0(其中λ∈R),由此可得方程组,从而可求定点的坐标;(2)求出A,B与定点的斜率,即可得到λ的取值范围;(3)先求出过A,B且斜率为 ![]() 的两条平行直线,再分直线l的斜率存在和不存在两种情况讨论即可.
的两条平行直线,再分直线l的斜率存在和不存在两种情况讨论即可.
【考点精析】解答此题的关键在于理解一般式方程的相关知识,掌握直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0).
(A,B不同时为0).

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在下图中的两条线段上,该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示. 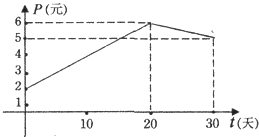
第t天 | 4 | 10 | 16 | 22 |
Q(万股) | 36 | 30 | 24 | 18 |
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)在(2)的结论下,用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几日交易额最大,最大值为多少?