题目内容

3．等比数列{an}的公比不为1，若a1=1，且对任意的n∈N*，都有an+1、an、an+2成等差数列，则{an}的前5项和S5=11．

分析 运用等差数列的性质可得2an=an+1+an+2，令n=1可得a3+a2-2a1=0，设公比为q，由等比数列的通项公式，解方程可得q，再由等比数列的求和公式，计算可得前5项和S5．

解答 解：对任意的n∈N*，都有an+1、an、an+2成等差数列，
即有2an=an+1+an+2，
令n=1可得a3+a2-2a1=0，设公比为q，
则a1（q2+q-2）=0．
由q2+q-2=0解得q=-2或q=1（舍去），
则S5=$\frac{{a}_{1}（1-{q}^{5}）}{1-q}$=$\frac{1-（-2）^{5}}{1-（-2）}$=11．
故答案为：11．

点评 本题考查等比数列和等差数列的通项、性质以及求和公式的运用，考查运算能力，属于基础题．

练习册系列答案
相关题目
10．在等差数列{an}中，已知a5=6，a8=15，求首项a1与公差d．
14．已知函数f（x）=x2-kx-8在[1，5]上具有单调性，则实数k的取值范围是（-∞，2]∪[10，+∞）．
11．求下列各题中的函数f（x）的解析式．
（1）已知函数y=f（x）满足2f（x）+f$（{\frac{1}{x}}）$=2x，x∈R且x≠0，求f（x）；
（2）已知f（x）是二次函数，且满足f（0）=1，f（x+1）=f（x）+2x，求f（x）．
18．（Ⅰ）计算：（a${\;}^{\frac{8}{5}}$•b${\;}^{\frac{6}{5}}$）${\;}^{\frac{1}{2}}$÷$\root{5}{{a}^{4}}$÷$\root{5}{{b}^{3}}$；
（Ⅱ）已知lga+lgb=2lg（a-2b），求$\frac{a}{b}$的值．
8．集合A={x|3≤x＜7}，B={x|2＜x＜10}，求A∪B，A∩B，（∁RA）∩B．
15．对于函数若f（x）=ax2+（b+1）x+b-2（a≠0），存在实数x0，使f（x0）=x0成立，则称x0为f（x）的“希望值”．
（1）当a=2，b=-2时，求f（x）的希望值；
（2）若对于任意实数b，函数f（x）恒有希望值，求实数a的取值范围．
12．已知f（x2-1）的定义域为$[-\sqrt{3}，\sqrt{3}]$，则f（x-1）的定义域为（　　）
A．[-2，1]B．[0，3]C．[-1，2]D．[-$\sqrt{3}$，$\sqrt{3}$]
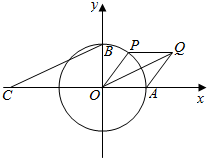13．如图所示，A，B分别是单位圆与x轴、y轴正半轴的交点，点P在单位圆上，∠AOP=θ（0＜θ＜π），C点坐标为（-2，0），四边形OAQP是平行四边形．
（1）若$\overrightarrow{CB}∥\overrightarrow{OP}$，求$|{\overrightarrow{OQ}}|$．
（2）求$sin（{2θ-\frac{π}{6}}）$的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网