题目内容
15.对于函数若f(x)=ax2+(b+1)x+b-2(a≠0),存在实数x0,使f(x0)=x0成立,则称x0为f(x)的“希望值”.(1)当a=2,b=-2时,求f(x)的希望值;
(2)若对于任意实数b,函数f(x)恒有希望值,求实数a的取值范围.
分析 (1)设x为希望值,则有2x2-x-4=x,变形为2x2-2x-4=0,解方程即可.
(2)将f(x)=x转化为ax2+bx+b-2=0.由已知,此方程有实根,则有△x≥0恒成立求解;
解答 解∵f(x)=ax2+(b+1)x+b-2(a≠0),
(1)当a=2,b=-2时,f(x)=2x2-x-4.
设x为其不动点,即2x2-x-4=x.
则2x2-2x-4=0.∴x1=-1,x2=2.即f(x)的不动点是-1,2.
(2)由f(x)=x得:ax2+bx+b-2=0.
由已知,此方程有实根,△x≥0恒成立,
即b2-4a(b-2)≥0.
即b2-4ab+8a≥0对任意b∈R恒成立.
∴△b≤0.,
∴16a2-32a≤0,
∴0≤a≤2.
点评 本题主要考查的知识点是二次函数的性质,方程的解法,方程根的情况以及垂直平分线定义的应用.其中根据已知中的新定义,构造满足条件的方程是解答本题的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
20.下列关系正确的是( )
| A. | 0∉N | B. | $\sqrt{2}∈Q$ | C. | ∅⊆{0} | D. | ∅={0} |
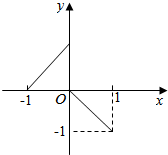 已知函数f(x)的图象如图所示.
已知函数f(x)的图象如图所示.