题目内容
13.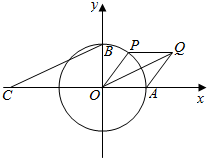 如图所示,A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),四边形OAQP是平行四边形.
如图所示,A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),四边形OAQP是平行四边形.(1)若$\overrightarrow{CB}∥\overrightarrow{OP}$,求$|{\overrightarrow{OQ}}|$.
(2)求$sin({2θ-\frac{π}{6}})$的值.
分析 (1)先求出P的坐标,再利用四边形OAQP是平行四边形,求$|{\overrightarrow{OQ}}|$.
(2)求出sinθ=y=$\frac{\sqrt{5}}{5}$,cosθ=x=$\frac{2\sqrt{5}}{5}$,可得sin2θ=2sinθcosθ=$\frac{4}{5}$,cos2θ=cos2θ-sin2θ=$\frac{3}{5}$,即可求$sin({2θ-\frac{π}{6}})$的值.
解答 解:(1)设P(x,y)由题意,y>0
因为$\overrightarrow{CB}$=(2,1),CB∥OP,
所以x=2y.又x2+y2=1,
解得y=$\frac{\sqrt{5}}{5}$,x=$\frac{2\sqrt{5}}{5}$,(4分)
因为四边形OAQP是平行四边形,
所以
$\begin{array}{l}\overrightarrow{OQ}=\overrightarrow{OA}+\overrightarrow{OP}\\|{\overrightarrow{OQ}}|=\sqrt{{{({\overrightarrow{OA}+\overrightarrow{OP}})}^2}}=\sqrt{2+\frac{{2\sqrt{5}}}{5}}\end{array}$(6分)
(2)sinθ=y=$\frac{\sqrt{5}}{5}$,cosθ=x=$\frac{2\sqrt{5}}{5}$,(8分)
所以sin2θ=2sinθcosθ=$\frac{4}{5}$,cos2θ=cos2θ-sin2θ=$\frac{3}{5}$.
故$sin({2θ-\frac{π}{6}})$=sin2θcos$\frac{π}{6}$-cos2θsin$\frac{π}{6}$=$\frac{4}{5}$×$\frac{\sqrt{3}}{2}$-$\frac{3}{5}$×$\frac{1}{2}$=$\frac{4\sqrt{3}-3}{10}$.(12分)
点评 本题考查三角函数的定义,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案(1)求每一个技术员被抽到的概率及该新产品研发小组中男、女技术员的人数;
(2)一年后研发小组决定选两名研发的技术员对该项研发产品进行检验,方法是先从研发小组中选一人进行检验,该技术员检验结束后,再从研发小组内剩下的三名技术员中选一人进行检验,若两名技术员检验得到的数据如下:
| 第一次被抽到进行检验的技术员 | 58 | 53 | 87 | 62 | 78 | 70 | 82 |
| 第二次被抽到进行检验的技术员 | 64 | 61 | 78 | 66 | 74 | 71 | 76 |
请问哪位技术员检验更稳定?并说明理由.