题目内容
18.(Ⅰ)计算:(a${\;}^{\frac{8}{5}}$•b${\;}^{\frac{6}{5}}$)${\;}^{\frac{1}{2}}$÷$\root{5}{{a}^{4}}$÷$\root{5}{{b}^{3}}$;(Ⅱ)已知lga+lgb=2lg(a-2b),求$\frac{a}{b}$的值.
分析 (Ⅰ)利用有理指数幂的运算法则求解即可.
(Ⅱ)利用对数运算法则化简求解即可.
解答 解:(Ⅰ)(a${\;}^{\frac{8}{5}}$•b${\;}^{\frac{6}{5}}$)${\;}^{\frac{1}{2}}$÷$\root{5}{{a}^{4}}$÷$\root{5}{{b}^{3}}$=${a}^{\frac{4}{5}-\frac{4}{5}}•{b}^{\frac{3}{5}-\frac{3}{5}}$=1 …(5分)
(Ⅱ)∵lga+lgb=2lg(2-2b),∴lgab=lg(a-2b)2.
∴ab=(a-2b)2,a2+4b2-5ab=0,($\frac{a}{b}$)2-5•$\frac{a}{b}$+4=0.
解之得$\frac{a}{b}$=1或$\frac{a}{b}$=4.…(8分)
∵a>0,b>0,若$\frac{a}{b}$=1,则a-2b<0,∴$\frac{a}{b}$=1舍去.
∴$\frac{a}{b}$=4.…(10分)
点评 本题考查对数运算法则以及有理指数幂的运算法则的应用,考查计算能力.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
9.已知全集U={1,2,3,4,5,6,7},M={1,3,5,7},N={2,5,6,7},则M∪(∁UN)=( )
| A. | {1,3,5,7} | B. | {1,2,4} | C. | {1,3,4,5,7} | D. | {1,3,4,5,6} |
13.若P点是以A(-3,0)、B(3,0)为焦点,实轴长为2$\sqrt{5}$的双曲线与圆x2+y2=9的一个交点,则|PA|+|PB|=( )
| A. | 4$\sqrt{13}$ | B. | 2$\sqrt{14}$ | C. | 2$\sqrt{13}$ | D. | 3$\sqrt{14}$ |
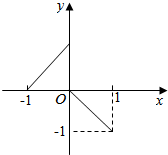 已知函数f(x)的图象如图所示.
已知函数f(x)的图象如图所示.