题目内容
已知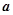 ,
,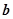 ,
,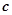 均为正实数,且
均为正实数,且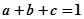 ,求证:
,求证: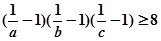 .
.
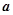 ,
,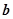 ,
,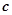 均为正实数,且
均为正实数,且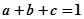 ,求证:
,求证: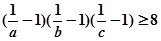 .
.见解析
利用条件和均值不等式,结合综合法的思想证明不等式成立
∵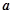 ,
,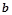 ,
, 均为正实数,且
均为正实数,且 ,
,
∴ ……………4分
……………4分
 , ………………………8分
, ………………………8分
当且仅当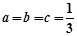 时,等号成立
时,等号成立
∵
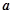 ,
,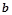 ,
, 均为正实数,且
均为正实数,且 ,
,∴
 ……………4分
……………4分 , ………………………8分
, ………………………8分当且仅当
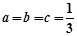 时,等号成立
时,等号成立
练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
题目内容
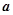 ,
,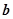 ,
,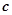 均为正实数,且
均为正实数,且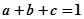 ,求证:
,求证: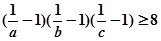 .
.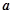 ,
,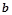 ,
, 均为正实数,且
均为正实数,且 ,
, ……………4分
……………4分 , ………………………8分
, ………………………8分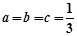 时,等号成立
时,等号成立
 春雨教育同步作文系列答案
春雨教育同步作文系列答案