题目内容
1.两平行线3x+4y-2=0和6x+8y+7=0之间的距离是$\frac{11}{10}$.分析 把直线方程3x+4y-2=0可化为6x+8y-4=0,由平行线间的距离公式可得答案.
解答 解:方程3x+4y-2=0可化为6x+8y-4=0,
由平行线间的距离公式可得:
两平行线间的距离d=$\frac{|-4-7|}{\sqrt{{6}^{2}+{8}^{2}}}$=$\frac{11}{10}$
故答案为:$\frac{11}{10}$
点评 本题考查平行线间的距离公式,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.【理】已知抛物线的方程为x2=2py(p>0),过点A(0,-1)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,1),连接BP,BQ,设BQ,BP与x轴分别相交于M,N两点.如果QB的斜率与PB的斜率的乘积为-3,则∠MBN的大小等于( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |
6.已知:a>0,b>0,不等式$a>\frac{1}{x}>-b$的解集是( )
| A. | $\left\{{x\left|{-\frac{1}{b}<x}\right.<0或0<x<\frac{1}{a}}\right\}$ | B. | $\left\{{x\left|{-\frac{1}{a}<x}\right.<0或0<x<\frac{1}{b}}\right\}$ | ||
| C. | $\left\{{x\left|{x<-\frac{1}{b}}\right.或x>\frac{1}{a}}\right\}$ | D. | $\left\{{x\left|{-\frac{1}{a}<x}\right.<\frac{1}{b}}\right\}$ |
10.已知两个等差数列{an}和{bn}的前n项和分别记为Sn和Tn,若$\frac{S_n}{T_n}=\frac{2n+1}{n+3}$,则$\frac{a_9}{b_9}$=( )
| A. | $\frac{7}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{37}{21}$ | D. | $\frac{19}{12}$ |
11.若抛物线的顶点在原点,焦点是双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1的顶点,则抛物线的方程是( )
| A. | y2=4x,y2=-4x | B. | y2=6x,y2=-6x | C. | y2=10x,y2=-10x | D. | y2=12x,y2=-12x |
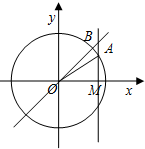 如图,角α的始边与x轴的非负半轴重合,终边与单位圆交于点A,直线MA垂直x轴于点M,B是直线y=x与MA的交点,设f(α)=$\overrightarrow{OA}•\overrightarrow{OB}$.
如图,角α的始边与x轴的非负半轴重合,终边与单位圆交于点A,直线MA垂直x轴于点M,B是直线y=x与MA的交点,设f(α)=$\overrightarrow{OA}•\overrightarrow{OB}$.