题目内容
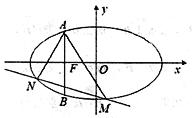
【题目】在平面直角坐标系xOy中，抛物线y=mx2﹣2mx+m﹣1（m＞0）与x轴的交点为A，B．
（1）求抛物线的顶点坐标；
（2）横、纵坐标都是整数的点叫做整点．
①当m=1时，求线段AB上整点的个数；
②若抛物线在点A，B之间的部分与线段AB所围成的区域内（包括边界）恰有6个整点，结合函数的图象，求m的取值范围．
【答案】
（1）
解：∵y=mx2﹣2mx+m﹣1=m（x﹣1）2﹣1，
∴抛物线顶点坐标（1，﹣1）．
（2）
解：①∵m=1，
∴抛物线为y=x2﹣2x，
令y=0，得x=0或2，不妨设A（0，0），B（2，0），
∴线段AB上整点的个数为3个．
②如图所示，抛物线在点A，B之间的部分与线段AB所围成的区域内（包括边界）恰有6个整点，
∴点A在（﹣1，0）与（﹣2，0）之间（包括（﹣1，0）），
当抛物线经过（﹣1，0）时，m= 
，
当抛物线经过点（﹣2，0）时，m= 
，
∴m的取值范围为 ＜m≤ ．
【解析】（1）利用配方法即可解决问题；
（2）①m=1代入抛物线解析式，求出A、B两点坐标即可解决问题．②根据题意判断出点A的位置，利用待定系数法确定m的范围．
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识，掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．
暑假作业暑假快乐练西安出版社系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】中央电视台为了解该卫视《朗读者》节目的收视情况，抽查东西两部各
个城市，得到观看该节目的人数（单位：千人）如下茎叶图所示其中一个数字被污损，
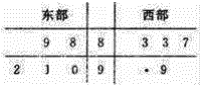
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率．
(2)随着节目的播出，极大激发了观众对朗读以及经典的阅读学习积累的热情，从中获益匪浅，现从观看节目的观众中随机统计了
位观众的周均阅读学习经典知识的时间（单位：小时）与年龄（单位：岁），并制作了对照表（如下表所示）：
年龄 |
|
|
|
|
周均学习成语知识时间 |
|
|
|
|
由表中数据，试求线性回归方程
，并预测年龄为
岁观众周均学习阅读经典知识的时间．
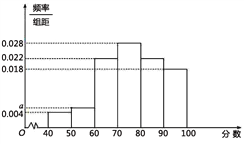
【题目】毕节市正实施“五城同创”计划。为搞好卫生维护工作，政府招聘了200名市民志愿者，按年龄情况进行统计的频率分布表和频率分布直方图如下：
分组（岁） | 频数 | 频率 |
[30,35) | 20 | 0.1 |
[35,40) | 20 | 0.1 |
[40,45) | ① | 0.2 |
[45,50) | ② | ③ |
[50,55] | 40 | 0.2 |
合计 | 200 | 1 |
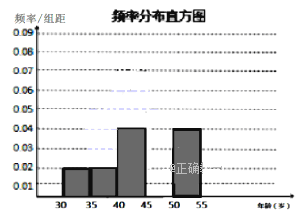
(1)频率分布表中的①②③位置应填什么数？补全频率分布直方图；
(2)根据频率分布直方图估计这200名志愿者的平均年龄．
