题目内容
【题目】某商店会员活动日.
(Ⅰ)随机抽取50名会员对商场进行综合评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100].
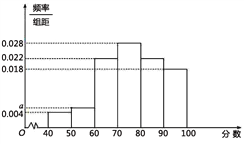
(1)求频率分布直方图中的值;
(2)估计会员对商场的评分不低于80的概率.
(Ⅱ)采取摸球兑奖的方式对会员进行返代金券活动,每位会员从一个装有5个标有面值的球(2个所标的面值为300元,其余3个均为100元)的袋中一次性随机摸出2个球,球上所标的面值之和为该会员所获的代金券金额.求某会员所获得奖励超过400元的概率.
【答案】(1)![]() (2)0.4.(3)
(2)0.4.(3) ![]()
【解析】试题分析:(Ⅰ)(1)利用频率分布直方图的面积之和为1,可得![]() 的值,(2)评分不低于80的概率即为最后两个条形的面积;(Ⅱ)记两个面值为300的球为
的值,(2)评分不低于80的概率即为最后两个条形的面积;(Ⅱ)记两个面值为300的球为![]() ,三和面值为100的球为
,三和面值为100的球为![]() ,从这5个球中随机抽取2个,所有可能的结果只有10种,会员所获得奖励超过400元的只有一种,由古典概型概率计算公式可得结果.
,从这5个球中随机抽取2个,所有可能的结果只有10种,会员所获得奖励超过400元的只有一种,由古典概型概率计算公式可得结果.
试题解析:解:(Ⅰ)(1)由![]() 得:
得: ![]() .
.
(2)由所给频率分布直方图知,50名会员评分不低于80的频率为![]() ,
,
所以会员对商场评分不低于80的概率为0.4.
(3)记两个面值为300的球为![]() ,三和面值为100的球为
,三和面值为100的球为![]() ,从这5个球中随机抽取2个,所有可能的结果只有10种,分别是
,从这5个球中随机抽取2个,所有可能的结果只有10种,分别是![]()
![]()
![]() ,
,
又因为所抽取的面值超过400的结果只有一种,故所求的概率为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】“北祠堂”是我校著名的一支学生乐队,对于2015年我校“校园周末文艺广场”活动中“北祠堂”乐队的表现,在高一年级学生中投票情况的统计结果见表:
喜爱程度 | 非常喜欢 | 一般 | 不喜欢 |
人数 | 500 | 200 | 100 |
现采用分层抽样的方法从所有参与对“北祠堂”投票的800名学生中抽取一个容量为n的样本,若从不喜欢“北祠堂”的100名学生中抽取的人数是5人.
(1)求n的值;
(2)若从不喜欢“北祠堂”的学生中抽取的5人中恰有3名男生(记为a1 , a2 , a3)2名女生(记为b1 , b2),现将此5人看成一个总体,从中随机选出2人,列出所有可能的结果;
(3)在(2)的条件下,求选出的2人中至少有1名女生的概率.